12

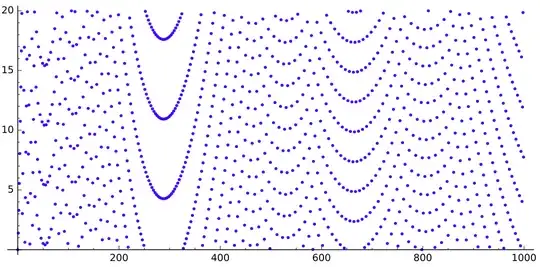
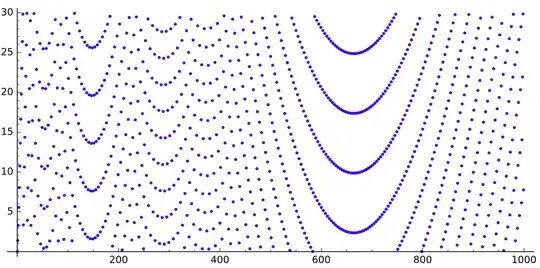
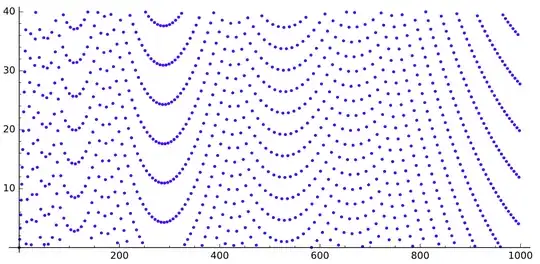
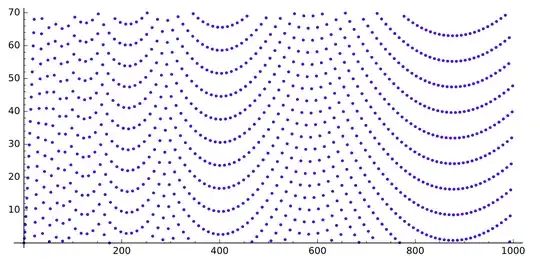
When I was thinking about my other question on the sequence

$$p(n)=\min_a\left\{a+b,\ \left\lfloor\frac {2^a}{3^b}\right\rfloor=n\right\}$$

I found an interesting link with the sequence

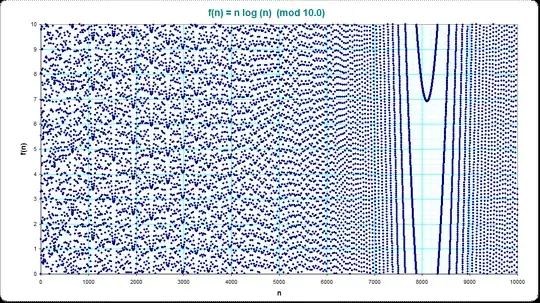
$$q(n)=\{n\log(n)\}=n\log(n)-[n\log(n)]$$

the fractional part of $n\log(n)$.

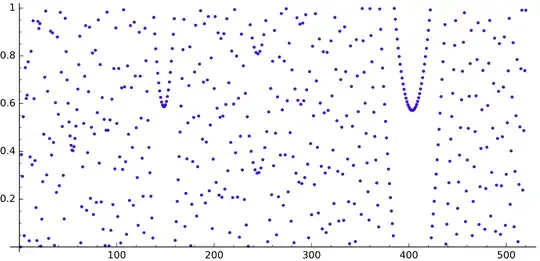
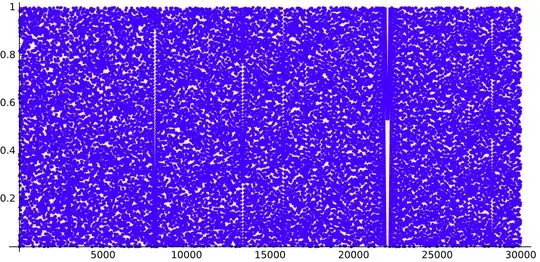
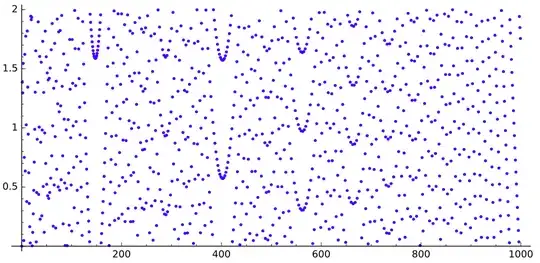
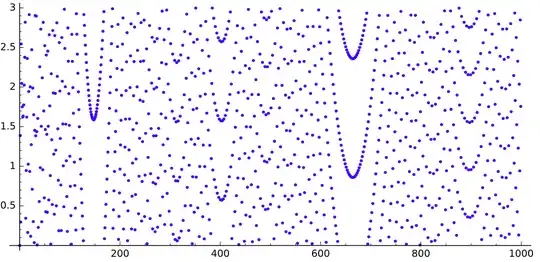
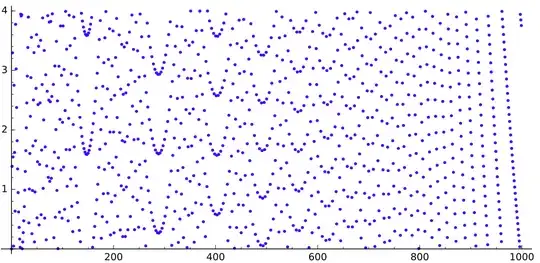
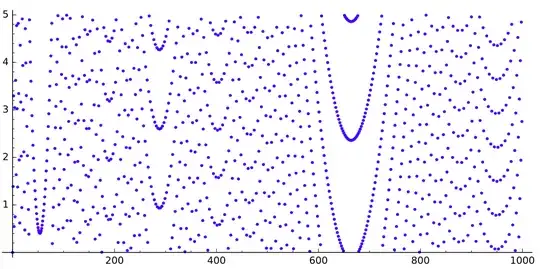
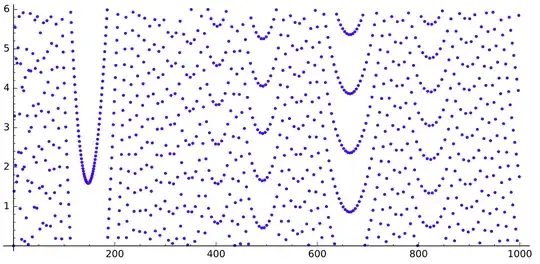
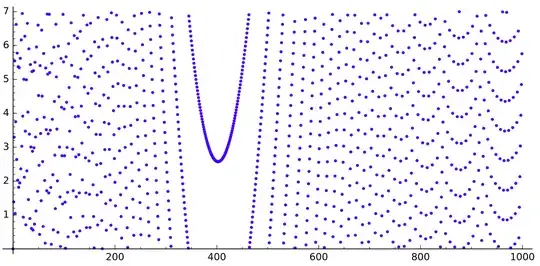
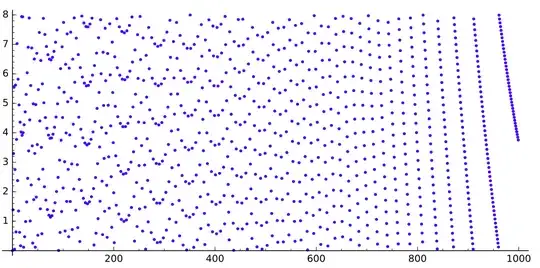
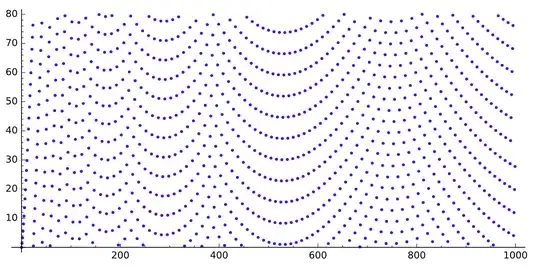
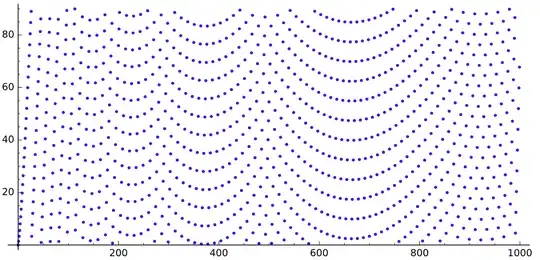
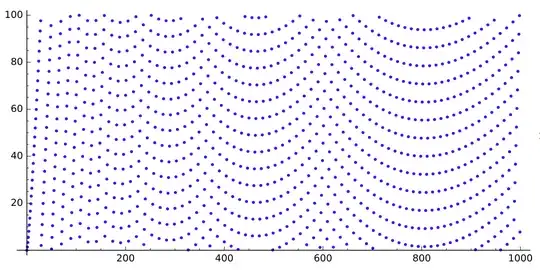
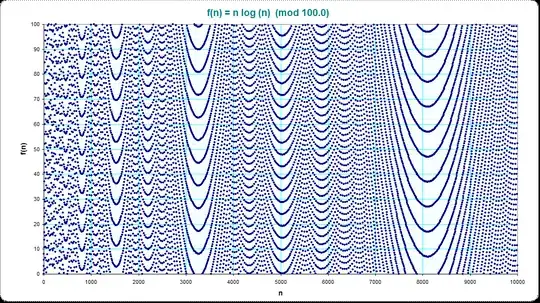
If we draw the sequence $q$, we get this (for $n$ up to $520$, $5\,000$ and $30\,000$ respectively):

enter image description here

enter image description here

enter image description here

We can see some gaps looking like parabolas.

What is causing those gaps? Why do they look like this?

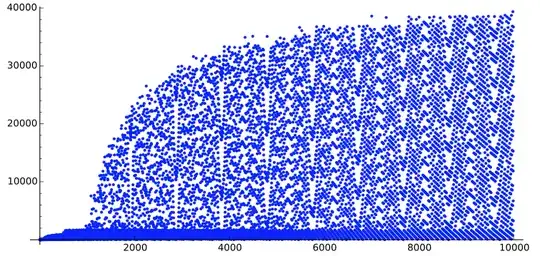
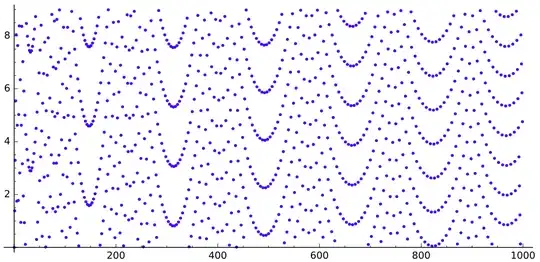
In my other question, we can observe similar structures:

enter image description here

An answer is telling me that it is due to the continued fraction of $\log2/\log 3$.

Could the two questions be linked?

Edit.

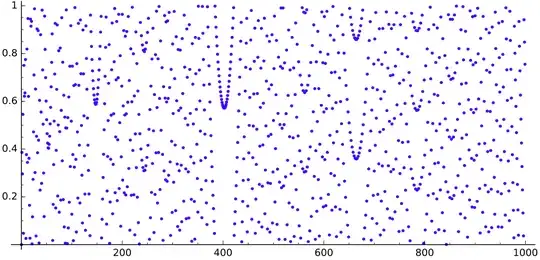
Thanks to Gottfried Helms idea, here is some more drawings with the moduli varying.

The moduli will take those values respectively:

$$1,2,3,4,5,6,7,8,9,10,20,30,40,50,60,70,80,90,100.$$

A modulus of $1$ corresponding to the fractional part.

enter image description here enter image description here enter image description here enter image description here enter image description here enter image description here enter image description here enter image description here enter image description here enter image description here enter image description here enter image description here enter image description here enter image description here enter image description here enter image description here enter image description here enter image description here enter image description here

Community
  • 1
E. Joseph
  • 15,066
  • Have you tried to take other moduli instead of $\pmod 1$, for instance $\pmod 2$ or $\pmod 10$? Perhaps the parabolas become even more prominent? – Gottfried Helms Feb 16 '17 at 01:14

2 Answers2

6

While this is not a complete answer, in order to get some insight to this phenomenon, consider the expression $$\{q(n+1)-q(n)\}=\{(n+1)\log(n+1)-n\log(n)\}=\{n\log(1+\frac{1}{n})+\log(n+1)\}$$ The first summand $n\log(1+\frac{1}{n})\sim 1-\frac{1}{2n}$ which is almost an integer and doesn't affect too much on that expression. It follows that $\{q(n+1)-q(n)\}\sim\{\log(n+1)\}$. So if $n+1\sim e^k$ or equivalently $\log(n+1)\sim k$ then the difference above is almost zero. You can see this in your diagram at $e^4\sim 54, e^5 \sim 148, e^5 \sim 403$ which is the bottom of the "parabolas". A little bit before it $\{q(n+1)-q(n)\}\sim\{\log(n+1)\}$ is a little bit smaller than 1 so that your graph is monotone decreasing, and similarly after it the graph is monotone increasing.

If for example $n+1\sim e^{5.5}\sim 255$ then the difference above is more or less 1/2 and then you will see two "parabolas" one above the other. The same argument will work for $n\sim e^{k +\frac{p}{q}}$ when you fix the rational $\frac{p}{q}$.

Ofir
  • 8,145
3

Not an answer but some more illustration (by my own couriosity)

I*ve looked at your function mod 10 and 100. Nice pictures... mod 10

mod 100

Ok, just for fun: "fine wood". Also see, how the picture can nicely be stacked vertically; here I stacked the mod-100 picture 3 times: finewood mod 100

Gottfried Helms
  • 35,815