11

Let $X_1, X_2, X_3, \ldots$ be an infinite sequence of i.i.d. Bernoulli($p$) random variables, and define the random real number $X = (0.X_1X_2X_3\ldots)_2$.

Question(s): What can be proved about the distribution of $X$ (for arbitrary $p$)? Are these singular distributions? What about their moments, etc.? Is it the case that $E[X]=p$?

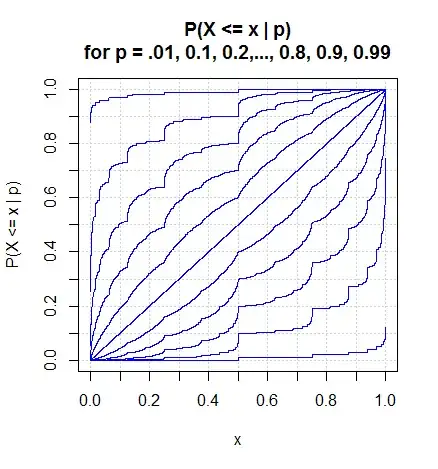
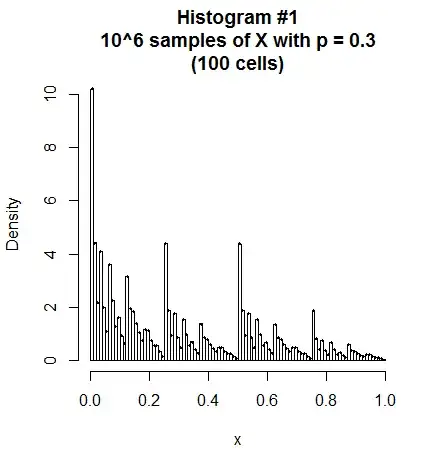
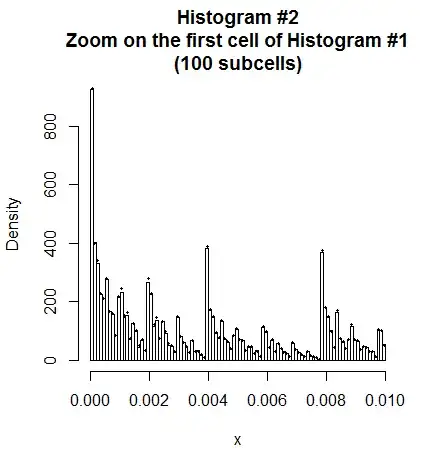
Here are some pictures from my simulations:

cdfs

In the above picture, the CDFs from upper left to lower right have increasing values of $p$. (In all cases, the simulations suggest that $E[X]=p$.)

hist1

hist2

In both histograms, the bars show the simulated random sample of i.i.d. $X$ values, and the small black dot near the top of each bar shows the computed value of $P(X\in \text{cell})$ for each cell, based on the infinite series for the CDF given below. (The agreement is excellent.)

There's evidently a fractal nature to these objects, and I'm unsure of the actual type of distribution, as to whether they are singular (rather than absolutely continuous or discrete). In any case, the slope of each CDF (other than for $p=\frac{1}{2}$) appears to be discontinuous at every "dyadic" point, i.e., at every $x=k\,2^{-m}$ for positive integers $k,m$.

Motivation: In a posting elswhere, I showed that if $p=\frac{1}{2}$, then $X\sim \text{Uniform}[0,1]$, so I naturally wondered about this more-general case. The same form of argument (via disjoint union) as presented there gives the following infinite series: $$\begin{align} P(X>x)&=P(X_1>x_1)\\ &+P(X_1=x_1\,\land\,X_2>x_2)\\ &+P(X_1=x_1\,\land\,X_2=x_2\,\land\,X_3>x_3)\\ &+\cdots\\ \\ &=p\,(1-x_1)\\ &+p\,^{x_1}\,(1-p)^{(1-x_1)}\,p\,(1-x_2)\\ &+p\,^{x_1+x_2}\,(1-p)^{(1-x_1)+(1-x_2)}\,p\,(1-x_3)\\ &+\cdots \end{align}$$ for any $x=(0.x_1x_2x_3\ldots)_2\in[0,1)$, where, WLOG, we always choose the unique binary representation of $x$ that has no infinite tail of $1$s. An algorithm that uses only the first $n$ bits of $x$ to approximate the CDF of $X$, viz., $P(X\le x)$, is therefore described by the following very simple pseudocode:

sum <- 0 
term <- 1 
for i in {1,...,n}:
    if x[i] == 1: 
        term <- term*p
    else: 
        sum <- sum + term*p
        term <- term*(1 - p) 
return (1 - sum)
Community
  • 1
r.e.s.
  • 15,537
  • 1
    $E[X]=p$ is easy to see from linearity of expectation: your r.v. is $\sum_{i=1}^\infty 2^{-i} X_i$ where $X_i$ are iid Bernoulli(p) r.v.s. My best guess would be that this distribution is singular, related to a Cantor distribution in some way, but I'm not sure. – Ian Aug 08 '16 at 02:07
  • @Ian - Aach... of course (about the expectation). – r.e.s. Aug 08 '16 at 02:09
  • 1
    You can also quickly compute the variance: $E[X^2]=\sum_{i=1}^\infty \sum_{j=1}^\infty 2^{-i} 2^{-j} E[X_i X_j]=\sum_{i=1}^\infty 2^{-2i} p + \sum_{i=1}^\infty \sum_{j=1,j \neq i}^\infty 2^{-i} 2^{-j} p^2$. Computing the sums we have $(p+2p^2)/3$. So the variance is $(p-p^2)/3$. – Ian Aug 08 '16 at 03:01
  • 3
    @r.e.s. Please read P. Billingsley "Probability and Measure" Third Edition. page 407. There is an exact answer to your question. For $p\neq 1/2$ it is singular. – theoGR Aug 08 '16 at 03:14
  • 1
    Note that if $f$ is the cdf of $X$, then $f$ satisfies the following functional equation: if $x \leq 1/2$, then $f(x) = p\cdot f(2x)$, and if $f \geq 1/2$, then $f(x) = p+(2p-1)f(2x-1)$. In particular, when $p=1/2$, this explicitly implies that $f(x)=x$. – shalin Aug 08 '16 at 03:36
  • 1
    See also the answer to this question: http://math.stackexchange.com/questions/1507188/probability-of-sum-n-1-infty-fracx-n2n-leq-p-for-bernoulli-sequenc/1507261#1507261 – shalin Aug 08 '16 at 03:48
  • 1
    I guess that from that functional equation you can get that $$f(\sum_1^{\infty} a_k2^{-k}) = \sum_1^{\infty} a_k (1-p)^{|{m<k:; a_m=1}|}p^{1+|{m<k:; a_m=0}|}$$ – shalin Aug 08 '16 at 03:52
  • I notice that some recent answers are at Measure induced on [0, 1] by infinite tosses of biased coin. – r.e.s. Sep 20 '16 at 14:17

1 Answers1

2

In answer to your questions:

  • $E[X] = \sum_i 2^{-i} E[X_i]= \sum_i 2^{-i} p = p$
  • $\text{Var}[X] = \sum_i \left(2^{-i}\right)^2 \text{Var}[X_i] = \sum_i 4^{-i}p(1-p) = \frac13p(1-p)$

For the cumulative distribution function, you can calculate (or arbitrarily well approximate) cumulative probabilities using:

  • $\Pr\left(X \le \frac{x}2\right) = (1-p)\Pr\left(X \le x\right)$ for $0 \le x \le 1$
  • in particular $\Pr\left(X \le 2^{-n}\right) = (1-p)^n$ for non-negative integer $n$
  • $\Pr\left(X \le \frac12+\frac{x}2\right) = (1-p)+p\Pr\left(X \le x\right)$ for $0 \le x \le 1$
  • in particular $\Pr\left(X \le 1-2^{-n}\right) = 1-p^n$ for non-negative integer $n$

Those create the fractal patterns in your graphs, and prevent the cumulative distribution function from being differentiable at any dyadic rational $x=\frac{m}{2^n}$ when $p \not \in \{0,\frac12,1\}$, as one of the left- and right-derivatives would approach zero and the other approach infinity, so these are singular distributions.

They also allow the calculation or approximation of individual values. For example

  • $\frac23 = 0.101010101\ldots_2$ and $\Pr\left(X \le \frac23 \right)= \dfrac{1-p}{1-p+p^2}$

  • $\frac1e = 0.010111100\ldots_2$ and $\Pr\left(X \le \frac1e \right)$ is slightly more than $1-p-p^2+p^3-p^5+2p^6-p^7$

Henry
  • 169,616
  • For what it is worth, the moment generating function seems to be $\displaystyle\prod_{i=1}^\infty \left(1-p+pe^{2^{-i} t}\right)$ – Henry May 18 '18 at 07:40