Why does the Ellipsograph/Trammel of Archimedes draw an ellipse, really?

Question

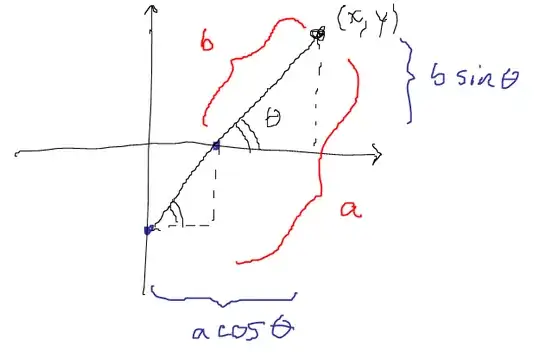
Here's a diagram of the device I mean, hard at work drawing an ellipse. I find this quite surprising, and would like to get to the bottom of things.

Essentially, a rod (black line in animation) is anchored to two sliders (in blue): One at an end, the other somewhere in the middle. The non-anchored end (black square) can move freely, tracing an ellipse, as the sliders move along perpendicular axes -- the end anchor along the minor axis, the interior anchor the major axis.

If you're willing to set up shop and start giving coordinates to the end that draws the ellipse (letting $a$ be the length of the rod, $b$ the distance from interior anchor to free end), it's not too hard to see that

\begin{align*} x &= a \cos \theta \\ y &= b\sin \theta, \end{align*}

and so in turn $$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1,$$

verifying the motion is indeed elliptical.

But I find this pretty unsatisfactory; until introducing coordinates, I had no reason to believe that an ellipse should be created. Even having introduced coordinates and verifying, I still find it very mysterious. What property of an ellipse am I missing that makes this device "obviously" draw an ellipse?

To put it another way: How could someone knowing only classical geometry (i.e., someone without coordinate geometry) have designed this machine to draw an ellipse? I am assuming that, being named after Archimedes, the device at least predates Descartes and thus coordinate geometry. Although, the runners do form something of a coordinate axis...

---

Compare this mysterious motion with the much more widely known method of putting pushpins down and tying one end of a string to each, pulling the string taut. This method is more apparent in how it generates an ellipse: the string has a fixed length which is the sum of distances from the pencil to each pushpin. This obeys the key and classically-known property that the sum of distances from foci to a point on the ellipse is a fixed distance.

Answer 1

It's intuitively clear that the curve has tangents which are perpendicular to each end of the major and minor axes and that the curve is continuous and symmetrical about each axis. So the trammel generates an oval which will at least look like an ellipse. If the trammel was intended as a practical instrument rather than a geometrical demonstration, it might not have mattered whether the curve actually was an ellipse. The design of the trammel may have been inspired by the approximate compass construction for the Three-Center Arch.

Answer 2

An ellipse is akin to a circle with a varying radius, ranging from the minor axis to the major axis. Every small section of an ellipse approaches a circle in the limit; or, closer to the way Archimedes would have put it:

Consider a small section of an ellipse. There are two concentric circles that the section of the ellipse lies entirely within. We can make the radii of these circles as close as we want, provided we look only at a sufficiently small section of the ellipse.

Call the up-down slider $S_1$ and the right-left slider $S_2$, their distance $s$, and the distance from $S_2$ to the pen $p$. When $S_1$ is at the ellipse's center $C$, the pen sweeps the exact path of a circle with radius $S_1 + S_2$.

Conversely, when $S_1$ is at its peak, $S_2$ will be at the center, and the pen sweeps the exact path of a circle with radius $S_2$.

This shows that at least those sections will match those of an ellipse with major axis $S_1 + S_2$ and minor axis $S_2$. What's left is to show that as the pen angle sweeps, the pen distance changes from $S_1 + S_2$ to $S_2$ at the exact same rate as the ellipse. This requires a definition of ellipse. Did Archimedes use the focus-directrix definition? Or did he have other ones, such as an angular definition?

Answer 3

A proof by was published in the 1600s by Johan de Witt and included as appendix to some editions of Descarte's Geometrie. The proof is purely Euclidean, not analytic, and was apparently written 10 years prior to the publication of Descarte's Geometrie.

The key step of the proof, if I understand it correctly, is as follows: Call the endpoints of the major axis $A$ and $A'$. For any point $P$ on the ellipse, let drop the perpendicular from $P$ to the major axis at $Q$. Then $$\frac{|PQ|^2}{|AQ||A'Q|}$$ is a constant (and indeed equal to the square of the ratio of the major axis to the minor axis).

From that, de Witt's proof follows:

Given two perpendicular lines AA’ and BB’ intersecting at O. In a trammel segment CD moves in a way that C is always on AA’ but D is always on BB’. Then if choose a fixed point P on CD (or extension of this segment), point P describes an ellipse with axis AA’ and BB’.

When C is at O, then P is in B, and when D is in O, P is in A, thus defining semiminor and semimajor axis of the ellipse. Let us draw PM⊥OA and DM⊥PM. Then PQ/PM = PC/PD (from similar triangles). But PC = OB = OB’ and PD = OA = OA’, so $|PQ|^2 / |PM|^2 = |OB|^2/|OA|^2$. But $|PM|^2 = |OA|^2 - |OQ|^2 =(OA-OQ)(OA+OQ) = AQ⋅A’Q$, and from here $|PQ|^2 = (|OB|^2 /|OA|^2)(AQ⋅A’Q)$, completing the proof.