17

Let $x \ge 0, y>0$ and \begin{align*} f(x,y)&=\sqrt{\dfrac{y}{y+x^2}}+4\sqrt{\dfrac{y}{(y+(x+1)^2)(y+(x+3)^2)}}\\[6pt] &\qquad +4\sqrt{\dfrac{y}{(y+(x-1)^2)(y+(x-3)^2)}}. \end{align*} Prove that $f(x,y) \le 3$.

I can prove when $x\ge 2, f(x,y) < 3$, but $f(x,y)=3$ when $x=0,y=3$, so the key part is $x\le 2 $

I found when $x<2, f'_x(y \ge 1.5) <0$ but I can't prove it as it has high degree equations.

And for $x<2,y<1.5$, I have no idea how to prove $f(x,y)<3$

River Li
  • 49,125
chenbai
  • 7,681
  • According to my calculations (I've always wanted to say that!), the other problem is equivalent to the inequality $g(x, y) \leqslant 3$, for all $x$ and all $y > 0$, where $g(x, y) = 2\sqrt{\frac{y}{y + (x+3)^2}} + 2\sqrt{\frac{y}{(y + x^2)(y + (x+1)^2)}} + 4\sqrt{\frac{y}{(y + (x-1)^2)(y + (x-3)^2)}}$. Can you confirm this equivalence? (I'll check my own work tomorrow, but I have to go to bed now.) – Calum Gilhooley Mar 22 '16 at 02:11
  • In terms of the complex number $z = (1 + x + i\sqrt{y})/2$, the pair of inequalities become $f(z) \leqslant 3$, $g(z) \leqslant 3$, where $f(z) = 2\Im(z)\left(\frac{1}{\lvert{z+1}\rvert} + \frac{1}{\lvert(z-1)(z-2)\rvert} + \frac{1}{\lvert{z}(2z-1)\rvert}\right)$, $g(z) = 2\Im(z)\left(\frac{1}{\lvert{2z-1}\rvert} + \frac{1}{\lvert(z-1)(z-2)\rvert} + \frac{1}{\lvert{z}(z+1)\rvert}\right)$. – Calum Gilhooley Mar 22 '16 at 02:46
  • 1
    this one is stronger than the other problem. If this one can be solved, the other one is solved also. – chenbai Mar 22 '16 at 03:43
  • 1
    The only reference I can find is: Walther Janous, "Further Inequalities of Erdos-Mordell Type", Forum Geometricorum 4 (2004), pp. 203–206 (PDF), citing p. 315 of D. S. Mitrinovic et al., Recent Advances in Geometric Inequalities, (Kluwer 1989; there's an expensive Springer reprint), which attributes to Klamkin and Meir the result that $\frac{\overline{h_1}}{m_1} + \frac{\overline{h_2}}{m_2} + \frac{\overline{h_3}}{m_3} \leqslant 3$, where $(\overline{h_1}, \overline{h_2}, \overline{h_3})$ is any permutation of $(h_1, h_2, h_3)$. – Calum Gilhooley Mar 24 '16 at 23:59
  • @CalumGilhooley thanks a lot, it is a very good reference for me. – chenbai Mar 25 '16 at 00:59

2 Answers2

1

No clue without an overview. With help of restrictions as found already by the OP, a contour plot / isoline chart has been produced for the function at hand:

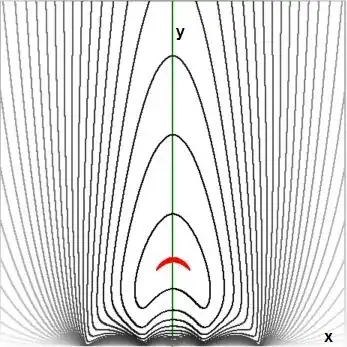
enter image description here

The $y$-axis is in $\color{green}{\mbox{green}}$. Our viewport is: 

  xmin := -6 ; xmax := 6;
  ymin := 0 ; ymax := 12;
The are 27 contour levels nivo, defined by: 

  for geval := 1 to 27 do
  begin
    nivo := geval/9.1;
The higher the level, the more black. The lower the level, the more white. The pixels in $\color{red}{red}$ are close to the conjectured maximum $=3$ . They are defined by: 

const
  eps : double = 0.0002;
  if (3-f < eps) and (3-f > 0) then
It is seen that the red spot is inside an area with very black lines, meaning that the function $f(x,y)$ is increasing there, towards the red spot.

Analysis. There is a mirror symmetry in the $y$-axis, as is clear from the figure but also from some algebra. Thus for all real $x$ and for all real $y > 0$ we have: $$ f(x,y) = f(-x,y) $$ It follows that: $$ \frac{\partial f(x,y)}{\partial x} = - \frac{\partial f(-x,y)}{\partial x} \quad \Longrightarrow \quad \left.\frac{\partial f(x,y)}{\partial x}\right|_{x=0} = - \left.\frac{\partial f(-x,y)}{\partial x}\right|_{x=0} \\ \Longrightarrow \quad \left.\frac{\partial f(x,y)}{\partial x}\right|_{x=0} = 0 $$ Meaning that all function gradients near the $y$-axis are tangent to it. Since the gradient vectors are perpendicular to the isolines, this can be observed in the figure as well. Now a sufficient condition for having a stationary point (maximum or minimum eventually) is that the total gradient be zero. But we already have $\,\partial f / \partial x = 0\,$ at the $y$-axis. Therefore substitute $\,x=0\,$ in $\,f(x,y)\,$ and only consider function values at the $y$-axis: $$ f(0,y)=1+8\sqrt{\frac{y}{(y+1)(y+9)}} $$ Extremes are found for: $$ \frac{d f(0,y)}{dy} = 0 \quad \Longrightarrow \\ \frac{1}{2} \left[ {\frac {1}{ \left( y+1 \right) \left( y+9 \right) }}-{ \frac {y}{ \left( y+1 \right) ^{2} \left( y+9 \right) }}-{\frac {y}{ \left( y+1 \right) \left( y+9 \right) ^{2}}} \right] \sqrt{\frac{\left( y+1 \right) \left( y+9 \right)}{y}} = 0 \\ \Longrightarrow \quad (y+1)(y+9) - y(y+9) - y(y+1) = -y^2 +9 = 0 \quad \Longrightarrow \quad y = \pm 3 $$ With the restriction $\,y > 0$ . Hence the only extreme at $\,(y,f(0,y))$ is $(3,3)\,$ and it is a maximum.
Picking up the comment by nbubis, prove that $f(0,2) < 3$ and $f(0,4) < 3$: $$ f(0,2)=1+8\sqrt{\frac{2}{(2+1)(2+9)}}=1+\sqrt{\frac{128}{33}}<1+\sqrt{\frac{128}{32}}\\ f(0,4)=1+8\sqrt{\frac{4}{(4+1)(4+9)}}=1+\sqrt{\frac{256}{65}}<1+\sqrt{\frac{256}{64}} $$

Han de Bruijn
  • 17,475
  • What's wrong with this proof? Just add two sample points at $y=1,4$ to show it's a maximum. – Nathaniel Bubis Mar 19 '16 at 18:34
  • 1
    Adding "sample points" like this is not needed in order to show that $f(0, y)$ is a maximum when $y = 3$, which in any case is only a matter of simple algebra. More importantly, the argument so far fails to show that $f(0, 3)$ is even a local maximum of $f(x, y)$ (it could still be a saddle point), let alone a global maximum, which is what is required. The difficulty of the question has not been addressed. – Calum Gilhooley Mar 19 '16 at 20:49
  • @nbubis: Adapted the answer accordingly. – Han de Bruijn Mar 20 '16 at 13:30
  • @CalumGilhooley: The question is only to prove that $f(x,y) \le 3$. There is not a single word about proving that $f(0,3)$ is a global maximum. – Han de Bruijn Mar 20 '16 at 13:35
  • @HandeBruijn Your reply baffles me, I'm afraid. We agree, of course, that $f(0, 3) = 3$; how, then, do you distinguish between on the one hand the statement that $f(x, y) \leqslant 3$ for all $x$ and all $y > 0$, and on the other hand the statement that $f$ attains its global maximum at $(0, 3)$? Have I entered an alternative universe in which these statements are not equivalent by definition? Are you perhaps merely observing the possibility, still left open, that also $f(x, y) = 3$ for some other values of $x$ and/or $y$? – Calum Gilhooley Mar 20 '16 at 13:54
  • @CalumGilhooley: I'm currently investigating the $\color{red}{\mbox{red banana}}$ environment in the picture :-) – Han de Bruijn Mar 20 '16 at 14:15
  • I feel like this proof is complete; all that remains is to show that the function stays below $3$ for the rest of the $xy$ plane, for $y \ge 0$. This amounts to taking the limit of the function as $x \to \infty$ by making the substitution $y=nx$, where $n \in (-infty, infty)$ is an arbitrary fixed constant. Then take the limit of the function as $y \to \infty$ and substitute $x=0$, and the proof is complete. – Rob Mar 21 '16 at 00:06
  • $\dfrac{y}{(y+1)(y+9)}=\dfrac{1}{\dfrac{9}{y}+y+10} \le \dfrac{1}{10+6} \iff \dfrac{9}{y}+y \ge 6 $ when $y=3$, which is clear. The trouble for me is even $x=1, f_{max}=2.99428,y=2.12362$ which is hard to prove without numeric method. when you set $y<1.5$, you will find the max some time is 2.9999. thanks for your work. – chenbai Mar 21 '16 at 08:57
  • @chenbai: Yes. Function behavior in the neighborhood of the maximum is extremely flat. Still working on it. – Han de Bruijn Mar 21 '16 at 09:00
  • @chenbai Where did you come across the problem? – Calum Gilhooley Mar 21 '16 at 09:36
  • I see the disclaimer has been dropped. (It read: "Disclaimer. Just evidence to ease a proof eventually, not a proof in itself." This part of the text was deleted 21 hours ago.) Is this now seriously being presented as an answer to the question? Again I'm getting the feeling of having gone mad or entered an alternative universe, because I see nothing even approaching a solution to the problem here! (If I really have gone mad, I apologise.) – Calum Gilhooley Mar 21 '16 at 10:56
  • Define $f_\text{oops}(x, y) = 1 + x^2 + 8\sqrt{y/((y + 1)(y + 9))}$. This is an even function of $x$, which coincides with $f(x, y)$ when $x = 0$. Your entire argument therefore applies to $f_\text{oops}$, and falsely concludes that $f_\text{oops}(x, y) \leqslant 3$ for all $x$ and all $y > 0$. – Calum Gilhooley Mar 21 '16 at 11:41
  • @CalumGilhooley I thought it was dropped by poster at first. Do you mean someone else deleted it? BTW the question comes from a triangle problem: $\dfrac{h_a}{m_a}+\dfrac{h_b}{m_c}+\dfrac{h_c}{m_b} \le 3$ Let $A(x,\sqrt{y}),B(-1,0),C(1,0)$ you will get it. – chenbai Mar 21 '16 at 13:02
  • @CalumGilhooley: Yes, I've deleted the Disclaimer. Because I find it sort of paranoia that a decent computer graphics output is supposed to be inferior to the minimal effort of copying and pasting output of a computer algebra system, thereby acting as if some tough analysis has been done. I've corrected more than a dozen typos in formulas at this forum. That alone shows that a "rigorous formal argument" is in no way more reliable than what our eyes can see in an informal pictural proof without words. – Han de Bruijn Mar 21 '16 at 15:47
  • @HandeBruijn Heh! Watch out, we paranoids are all in it together, and are out to get you! :) – Calum Gilhooley Mar 21 '16 at 17:07
  • @chenbai I see this question also remains unanswered. – Calum Gilhooley Mar 21 '16 at 17:36
0

Here is a proof:

Using Cauchy-Bunyakovsky-Schwarz inequality, we have \begin{align*} [f(x, y)]^2 &\le \left(\frac{3y}{4(x^2 + y)} + \frac{y}{y + (x + 1)^2} + \frac{y}{y + (x - 1)^2}\right)\\ &\qquad \times \left(\frac43 + \frac{16}{y + (x + 3)^2} + \frac{16}{y + (x - 3)^2}\right). \end{align*} It suffices to prove that \begin{align*} &9 \ge \left(\frac{3y}{4(x^2 + y)} + \frac{y}{y + (x + 1)^2} + \frac{y}{y + (x - 1)^2}\right)\\ &\qquad \times \left(\frac43 + \frac{16}{y + (x + 3)^2} + \frac{16}{y + (x - 3)^2}\right) \end{align*} or \begin{align*} &16\,{y}^{5}+ \left( 91\,{x}^{2}+64 \right) {y}^{4}+ \left( 204\,{x}^{4 }+60\,{x}^{2}-672 \right) {y}^{3}\\ &\qquad + \left( 226\,{x}^{6}-612\,{x}^{4}- 1038\,{x}^{2}+576 \right) {y}^{2}\\ &\qquad + \left( 124\,{x}^{8}-1148\,{x}^{6}+ 2388\,{x}^{4}-612\,{x}^{2}+1296 \right) y\\ &\qquad +27\,{x}^{10}-540\,{x}^{8}+ 3186\,{x}^{6}-4860\,{x}^{4}+2187\,{x}^{2} \ge 0. \tag{1} \end{align*}

My proof of (1) is not nice. nexu@AoPS gave a very nice SOS (Sum of Squares) proof of (1): \begin{align*} &16\,y^5+\left( 91\,x^2+64 \right) y^4+\left( 204\,x^4+60\,x^2-672 \right) y^3\\ &\qquad +\left( 226\,x^6-612\,x^4-1038\,x^2+576 \right) y^2 \\ &\qquad +\left( 124\,x^8-1148\,x^6+2388\,x^4-612\,x^2+1296 \right) y\\ &\qquad +27\,x^{10}-540\,x^8+3186\,x^6-4860\,x^4+2187\,x^2 \\ =\,& \frac{y\left( 38x^4+55x^2y-209x^2-6y^2-8y+78 \right) ^2}{38}\\ &\qquad +\frac{x^2\left( 27x^4+43x^2y-270x^2-20y^2-21y+243 \right) ^2}{27} \\ &\qquad +\frac{800039x^2y^2(y-3)^2}{28356}+\frac{1843x^2y(y-3)^2}{43}+175y^2(x^2+y-3)^2\\ &\qquad +\frac{142709197y(x^2+y-3)^2}{1310482} +\frac{x^2y^2(4726x^2+3583y-10749)^2}{255204}\\ &\qquad +\frac{y\left( 7683x^2y-23769x^2+857y^2-5862y+9873 \right) ^2}{875862} \\ &\qquad +\frac{y\left( 1579185x^2+655241y^2-2352261y+1159614 \right) ^2}{30205299618}\\ &\qquad+\frac{x^2y(86x^2+79y-237)^2}{43} \\ \ge\,& 0. \end{align*}

We are done.

River Li
  • 49,125