1

My understanding is that Burgers' equation is a prototype for wave breaking: Solution $u(x,t)$ stays bounded as its derivative $u_x(x,t)\to\infty$. I solved $$u_t+uu_x=0,\,\,\, u(x,0)=-x,\,\,\, x\in[0,1],$$ and got $$u(x,t)=-\frac{x}{1-t},\,\,\, u_x(x,t)=-\frac{1}{1-t}.$$ Surely $u_x(x,t)\to-\infty$ everywhere in $[0,1]$, but $u$ also does at any $x\in(0,1]$. I know $u$ along characteristics is constant, in this case it equals $-x$, and at the singularity time, $t^*=1$, all characteristics are converging to $x=0$, where $u$ is zero. So there is steepening happening in $u$ at $x=0$, but $u$ is not bounded for $t\in[0,t^*)$.

EditPiAf
  • 21,328
user210190
  • 157

1 Answers1

2

Since the Burgers equation is nonlinear, there can be infinitely many solutions in the sense that you are considering (just taking the derivatives and plugging them in the equation).

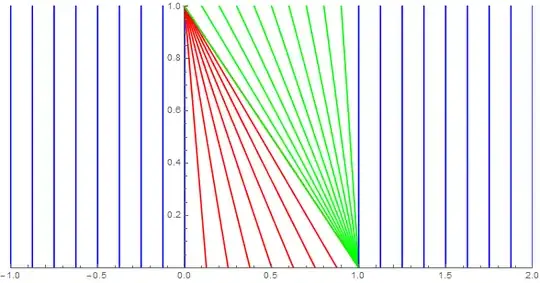
In order to select the solution to the equation, one has to be more restrictive on what can be considered a solution. In that sense, shocks are defined, mass conservation is imposed... and rarefaction waves appear. In your case, a rarefaction wave arises in $(x=1,t=0)$, opening to the left, which controls the height of the peak you are mentioning. In the graph below (characteristics in $x$ vs. $t$), you can see that, while the non-zero part of the initial data moves into a shock at $t=1$ (in red), a rarefaction wave appears in the empty space that it appears behind it.

enter image description here

I really like how this is explained in Partial Differential Equations by Lawrence C. Evans, but you can find lots of notes about the topic in Google.

EDIT: In that book, you can find a theorem that describes the behavior of solutions to the Burgers equation in the whole spatial domain. It says that for bounded and summable initial data (hence, vanishing at $\pm\infty$), there exists $C>0$ such that $|u(x,t)|\le Ct^{-1/2}$ for all $x\in\mathbb{R}$ and $t>0$.

Moreover, the dynamics of the Burgers equation push all such initial data (whatever their shape is) towards a function called N-wave, which IMHO is fascinating.

AugSB
  • 5,107
  • Thanks! I found that with $u_0(x)=x(1-x)$ and boundary conditions $u(0,t)=u(1,t)=0$, the solution $u$ nos stays bounded on $0\leq x\leq1$ but its derivative goes to $-\infty$. But I am still wondering what types of initial conditions and/or boundary conditions will lead to that as opposed to both $u$ and $u_x$ diverging at some finite time. – user210190 Feb 25 '16 at 14:58
  • I do not think I understood what is your doubt. Are you considering the whole spatial domain or just a bounded interval? Note that it is quite tricky to impose boundary conditions to this type of equations, since not all of them are admissible. On the other hand, if you consider the whole spatial domain, any compactly supported and bounded initial data remains bounded (with this bound going down to 0) and preserves the mass. – AugSB Feb 25 '16 at 15:38
  • I was considering two settings, one with domain $[0,1]$, $u$ zero at the endpoints and $u(x,0)=x(1-x)$. The other on the same unit interval, but $u(x,0)=-x$ and no boundary conditions. For the first one, integrating the equation between 0 and 1 leads to the mean of $u$ being conserved. May be that and vanishing at the boundary forces the solution to stay bounded (?). – user210190 Feb 25 '16 at 16:24
  • Yes. Solutions to the Burgers equation with bounded initial data vanishing at the boundaries (or at $\pm\infty$) remain bounded. – AugSB Feb 25 '16 at 17:33
  • I added a short paragraph at the end regarding this behavior. Please, accept the answer if you feel it fulfills your requirements. – AugSB Feb 26 '16 at 08:44