1

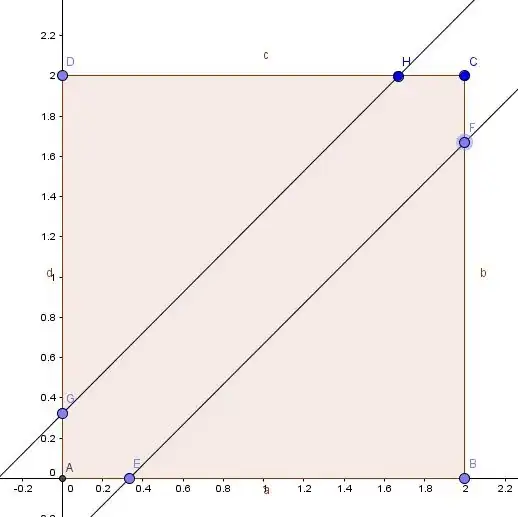
Consider two sentries that are patroling on a road that is 2 miles long. They are sent to points chosen independently and at random on the road. I want to find the probability that the sentries will be less than $\frac{1}{3}$ mile apart when they reach their respective points.

I imagine two sentires $i$ and $j$, and I let $X_i$ be the random variable that represents the point $i$ is assigned to and $X_j$ be the random variable that represents the point $j$ is assigned to. Obviously, from the discussion of the problem, $X_i, X_j \sim U[0,2]$, where $0$ represents the beginning of the road and $2$ represents the end of the two miles of the road. What we need to find is $$P(|X_i-X_j| < \frac{1}{3}) = P(\frac{-1}{3} < X_j-X_j < \frac{1}{3}).$$ However, I am having some issues figuring out how to alter this problem in order to make this a probability that considers only one random variable as an input. Any suggestions on how to go about doing this?

Daniel Murphy
  • 13

2 Answers2

3

Consider a square of $2 \times 2$. Plot the position of the first sentry on the horizontal axis and the second one on the vertical axis. Now the sample space is the total area of the square which is $4$. Can you draw the necessary lines (band) which represents the distance between the two is less than $\frac{1}{3}$. All you have to do is to now calculate the area of this band. The bands are drawn as parallel lines $\frac{1}{3}$ distance from the diagonal ($x=y$). The area of the left out portion is two triangles, which add up to $\frac{25}{9}$ and hence the area of the band is $\color{blue}{\frac{11}{9}}$ and the probability is $\color{blue}{\frac{11}{36}}$.

Thanks

to Ross Millikan for providing the diagram in GeoGebra.

Links

Please take a look here for a related problem and solution.

enter image description here

Community
  • 1
Shailesh
  • 3,908
0

The quantity $(X_i - X_j)$ is a random variable.

Perhaps you already know the distribution of $X_i + X_j$ if $X_i$ and $X_j$ are iid variables, $X_i \sim U[0,2]$ and $X_j \sim U[0,2]$.

Now consider $Y = 2 - X_j$. Hopefully it is not too hard to see that $Y \sim U[0,2]$ too. If you know the distribution of the sum of two iid $U[0,2]$ variables, you know the distribution of $X_i + Y$.

Notice that $X_i + Y = X_i + (2 - X_j)$. This should tell you something about the distribution of $X_i - X_j$.

David K
  • 108,155