14

It's easy to bound a volume of a half. For example, the points $(0,0,0),(0,0,1),(0,1,0),(3,0,0)$ can do it. The problem is harder if no two points can be further than 1 apart. Bound a volume of 1/2 with a diameter $\le 1$ point set.

With infinite points at distance 1/2 from the origin, a volume of $\pi/6 = 0.523599...$ can be bound. But we want a finite point set. What is the minimal number of points?

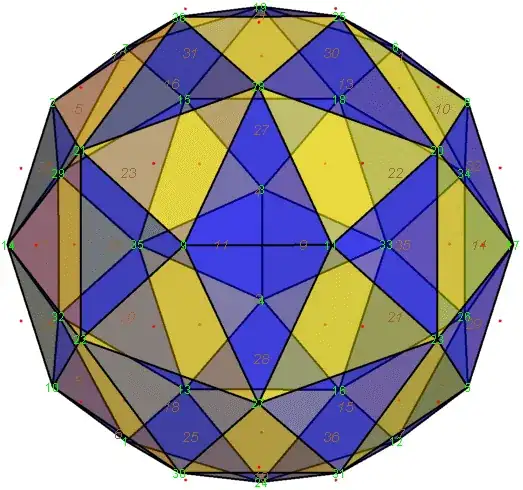
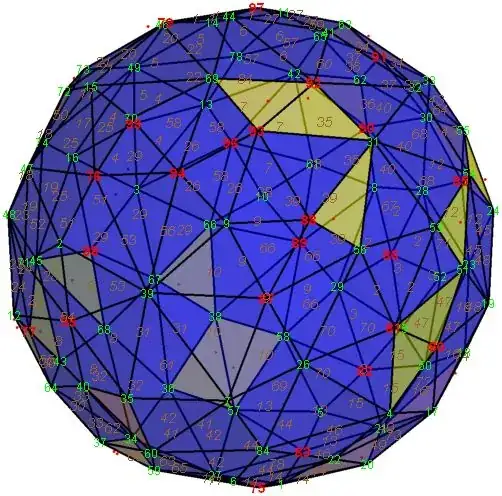
(A 99 point set used to be here. See Answers for a much better 82 point set)

Here's a picture of the hull. Each vertex is numbered. Green vertices have one or more corresponding blue faces with vertices at distance 1. Each blue face has a brown number giving the opposing green vertex. Red vertices and yellow faces lack a face/vertex pairing.

99 points

Some may think that Thomson problem solutions might give a better answer. The first diameter 1 Thomson solution with a volume of 1/2 is 121 points with volume .500069.

These points will not fit in a diameter 1 sphere, but the maximal distance between points is less than 1. Similarly, a unit equilateral triangle will not fit in a diameter 1 circle.

Is 99 points minimal for bounding a volume of 1/2 using a point set with diameter 1? Or, to phrase it as a hypothesis:

99 Point Hypothesis
99 points of diameter 1 in Euclidean space.
99 points with a volume of a 1/2.
Take one off, move them around (without increasing diameter)
You can't get a volume of 1/2 any more.

Ed Pegg
  • 21,868
  • I had an answer, but then deleted it after realizing that a point set with diameter $d$ might not be inscribable in a sphere of diameter $d$. Indeed, 70 of the 110 points in your example lie outside the sphere of radius $1/2$. It might be worth noting this property of your point-set in your post. After all, the option to go outside the sphere gives us options not available to Thomson problem solutions. – dshin Jan 17 '16 at 23:22
  • I saw your answer and liked the information in it a lot, even though it was for a related problem. – Ed Pegg Jan 18 '16 at 15:34
  • Ok, I adjusted my answer and revived it. – dshin Jan 18 '16 at 15:50

4 Answers4

7

(Update)

My current result is $82$ points:

consider this point set:

pts = {
{39331, -1787,  125739},
{-42020,    -78476, 96709},
{97017, -83209, 30835},
{-17033,    70737,  109597},
{-54599,    29504,  115688},
{-69547,    63866,  91701},
{-84862,    -62280, -80052},
{111630,    -49662, -51118},
{110858,    44843,  -58218},
{7570,  -94324, 91248},
{115828,    -36578, 50910},
{-103422,   33617,  73525},
{13903, 130088, -24865},
{-48488,    -30540, -119577},
{13546, 105208, 78574},
{92754, -90941, -22055},
{-87842,    -12726, -97961},
{17890, -95311, -90222},
{-32617,    127358, -17688},
{-83770,    -100939,    6478},
{-67513,    -103415,    -46172},
{-15435,    70574,  -111233},
{42948, 122369, 28253},
{82827, -31757, -98975},
{-8841, 14824,  130515},
{-31918,    -116156,    52485},
{-124638,   33189,  26548},
{46151, -58101, 108697},
{-107711,   76927,  -3256},
{8590,  -131155,    -3832},
{-2349, -45047, 123671},
{-67052,    113066, 17470},
{-49845,    -26471, 118738},
{45038, -56580, -110986},
{124167,    -45279, 903},
{60780, -115738,    12319},
{-109374,   -68092, -27125},
{-40207,    -124921,    2722},
{74952, 40665,  100449},
{88162, -58830, 78010},
{60461, 114907, -29946},
{110136,    -3355,  -73936},
{70896, 79060,  -79787},
{56554, -97875, 67358},
{72446, -84584, -71147},
{30586, 57713,  114256},
{-15936,    -120088,    -52161},
{-480,  -46761, -124154},
{-72908,    103917, -38653},
{-101424,   28721,  -80454},
{-45115,    103290, 68859},
{41881, -117921,    -41667},
{-74575,    -93889, 53049},
{108114,    53390,  54482},
{15266, -123265,    42434},
{40723, -3854,  -126221},
{90334, 94409,  22158},
{96396, 85431,  -32579},
{-63349,    75478,  -88497},
{122169,    52183,  -1811},
{108487,    5280,   74810},
{-88785,    -956,   96779},
{-7851, 14221,  -131625},
{64857, 88850,  73124},
{23713, 102177, -81511},
{129972,    1413,   -27143},
{-119337,   -14421, 52312},
{-88103,    -51438, 82718},
{-10887,    127563, 33645},
{33805, 54367,  -116181},
{-102814,   64657,  -52366},
{-126644,   25744,  -26822},
{-25275,    110536, -68979},
{-112785,   -59627, 30034},
{-129858,   -19908, 289},
{-36740,    -84005, -95750},
{78058, 29755,  -103069},
{-118373,   -22382, -53597},
{-55526,    28946,  -116699},
{-94065,    79056,  48080},
{80742, -15619, 102763},
{129505,    8123,   26059}
}

Then (Mathematica code)

Volume[ConvexHullMesh[pts]]

is $\approx 9.00744\times10^{15}$.

And Mathematica sketch:

ConvexHullMesh[pts]]

82 points convex hull

Another picture. If all vertices of a face are at distance one from another vertex, the face is colored blue.

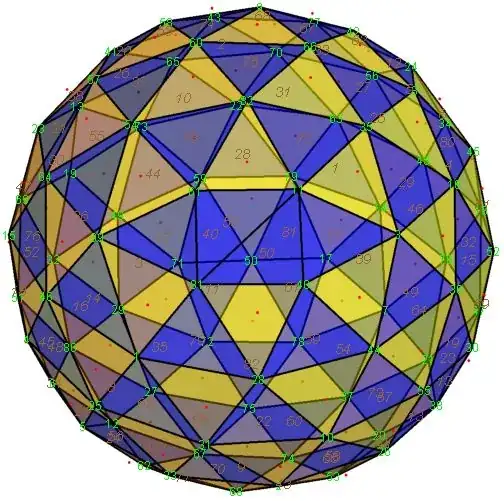
82 point polyhedron

Since all point coordinates are integer, then one can write it directly (with arbitrary small computational errors):

$$Diameter = \sqrt{68\;719\;348\;253} \approx 262\;143.\;754\;938;$$ $$Volume = \dfrac{54\;044\;635\;971\;533\;362}{6} \approx 9\;007\;439\;328\;588\;893.\;666\;667.$$

If multiply all coordinates by $\dfrac{1}{2^{18}}$, then we'll get:

$$Diameter = \frac{\sqrt{68\;719\;348\;253}}{262\;144} \approx 0.999\;999\;065;$$ $$Volume = \dfrac{54\;044\;635\;971\;533\;362}{2^{54}\times 6} \approx 0.\;500\;013\;326.$$

Note: when add any point (with real coordinates) rather close to (the center of) any face, one will get the set of $83, 84, ...$ points with described property.

Ed Pegg
  • 21,868
Oleg567
  • 17,740
  • I hope that my computations are without errors, but it would be great to test this result more accurately. – Oleg567 Feb 10 '16 at 10:15
  • Amazing, that impressively beats my 96 point solution. How did you find this, and how long did it take you? I did check your point set, and it works. – Ed Pegg Feb 10 '16 at 13:54
  • 1
    @Ed, I use C++ for search, and Mathematica for check. (I still don't know which Mathematica function calculates diameter of point set). In a few words: first, I "sieve" points with real coordinates randomly into layer $L = {(x,y,z): r_1 \le \sqrt{x^2+y^2+z^2} \le r_2}$, and then move them slightly. And recalculate convex hull each iteration. Say, $r_1 = 0.495$, $r_2 = 0.5$; then calculate $D_0$ $-$ diameter, $V_0$ $-$ volume, and then focus on the value $\dfrac{V_0}{D_0^3}$. It takes a few hours, if memorize current not bad solutions. – Oleg567 Feb 10 '16 at 14:31
  • If you've got best point sets for other values of $n$ handy, I'd love to see them. edpegg @ gmail – Ed Pegg Feb 10 '16 at 15:06
4

The current best known volume bound by 97 points is .4999609.

Currently, 98 points is the lower bound, with a current best volume of .5001309. Here's a simplified version of 98 points bounding a volume of 1/2.

pts = 
({{25161,15239,15738}, {-19559,26175,-6775}, {-4006,24157,-22572},   
{26243,20473,1977}, {3626,21357,25058}, {-16176,-20481,19867},   
{19600,24155,-12113}, {-20547,-23666,-10570}, {15495,-4185,28992},   
{-30124,-3246,14209}, {20518,-25644,-4873}, {-27314,-16747,8407},   
{24128,-1894,-22531}, {28918,-5278,15688}, {-9651,-30430,-8794},   
{32124,-8719,2667}, {7,-28881,15714}, {-27983,17284,5117},   
{31307,-5904,-8466}, {-29112,-13355,-7321}, {-11197,31241,2423},   
{-16493,-6895,-28142}, {-4835,-19067,26682}, {-27426,9201,16379},   
{-14201,11757,-27212}, {-13743,26726,14584}, {15279,29455,544},   
{23529,14005,-19238}, {3316,13250,-29746}, {32829,6364,-1267},   
{-17854,20459,-18567}, {23584,2651,22825}, {-31684,1388,-8352},   
{-27907,13905,-10730}, {-20649,-25299,3031}, {-7914,13803,28914},   
{-5685,31345,-9492}, {8966,26190,-18664}, {13899,26052,14660},   
{-19436,-5349,26308}, {12582,-26252,15883}, {9,3354,32858},   
{15269,12403,25837}, {-27834,-4988,-17084}, {-32368,2810,4363},   
{-18997,10095,25337}, {2653,-27021,-19141}, {14688,14913,-25846},   
{31456,5955,8605}, {22783,-19010,-14896}, {7504,-30451,-9382},   
{11921,-30012,5350}, {-6237,3312,-32379}, {5452,32220,3112},   
{4892,30443,-11704}, {20633,-13337,22304}, {13320,-19143,-23609},   
{-15014,-19141,-22978}, {1043,-33106,290}, {26794,-18693,4769},   
{-22610,4416,-23628}, {-11418,-29433,9363}, {-1517,-12798,-30638},   
{23056,-19104,13931}, {10706,-3817,-31400}, {7894,7519,30955},   
{5255,-14276,29698}, {-1278,31511,10073}, {-9977,-7220,30694},   
{-6921,22257,22989}, {29137,11121,-9805}, {-31068,-7994,1171},   
{-18843,17399,20269}, {-8660,-25176,-19425}, {12922,-18519,24195},   
{27836,-15187,-6057}, {-21640,22315,9878}, {-6851,-32147,3772},   
{-23691,-11945,18070}, {4488,2283,-32516}, {14245,5686,-28818},   
{-22214,-12745,-19863}, {22760,-11594,-20279}, {-12368,2766,29586},   
{5081,28759,15175}, {4609,-19768,-25959}, {-1159,-8679,31850},   
{13750,-25002,-14800}, {-24581,10464,-18734}, {4255,-22632,22566},   
{28756,3237,-13827}, {-9454,-14279,-28365}, {19317,-24852,6639},   
{12130,-11039,-28322}, {-6116,-4669,-31895}, {-30516,9944,-2126},   
{-24217,1636,21574}, {20094,24320,7885}} * 1/(2^20 +2))//N;

Max[EuclideanDistance[#[[1]], #[[2]]] & /@ Subsets[pts, {2}]]  
0.999997 

Volume[ConvexHullMesh[N[pts]]]  
0.500044

Here's a picture of a non-simplified version of the 98 points. All three vertices of a blue triangle are at distance 1 from a vertex on the other side.

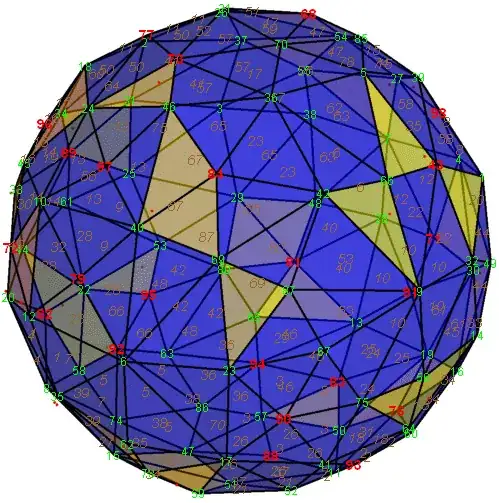
98 points bounding a volume of 1/2

A similar picture for 36 points, which bounds a volume of 0.4699687. I believe this is optimal. Some believed-optimal solutions for 7, 8, 9, 10, 11, and 16 points are at my blog article and at the demo biggest little polyhedron, which has been updated.

biggest little polyhedron for 36 points.

Ed Pegg
  • 21,868
2

A related question is to ask the volume of the largest $n$-vertex polyhedron which can be inscribed in a sphere of given size. It is important to recognize that this is a different problem, as a polyhedron of diameter $d$ is not generally inscribable in a sphere of diameter $d$. To illustrate, your 110-vertex polyhedron actually contains 70 points outside of the diameter-$1$ sphere centered at the origin (I have not verified whether some other diameter-$1$ sphere not centered at the origin might contain fewer than 70 vertices of your polyhedron in its exterior).

With that said, the question of the largest $n$-vertex polyhedron which can be inscribed in a sphere of a given size is asked here. Its solution is unknown for $n>8$, which hints that your problem might be hard to solve.

The accepted answer to that question links to a 1994 page entitled "Maximal Volume Spherical Codes", which appears to use Thomson problem solutions for their putatively optimal arrangements, as they list $n=121$ as the smallest $n$ which breaches the $1/2$ threshold.

Community
  • 1
dshin
  • 1,555
  • For that related problem, I get that the volume for 16 points is exactly Root[-3784084398958182400 + 1457973565222551552 #1^2 - 179253470562877440 #1^4 + 7618104759214080 #1^6 - 74727572486976 #1^8 + 847288609443 #1^10 &, 5] = 2.88645539227451858, which matches the Sloane results. My methods match their results for 8, 9, and 16, which were among my strong results, so I would say those results are solved. My other superstrong result is for n=36, so I'll need to check that next. – Ed Pegg Jan 18 '16 at 16:40
2

Just for fun, I got down to 162 points and a volume of .5058 by starting with a triangulation of a Icosahedron and subdividing each triangle into 4 smaller triangles twice.

I improved my own first try by using a Fibonacci Sphere for n points I than calculated the volume for 100 points up to 150 poimts. At 128 points, it goes over 0.5 num = 127 volume = 0.49984077982 num = 128 volume = 0.500172211602.

hardmath
  • 37,715
Andreas Gammel
  • 21