This is supposed to be a comment but I would like to post a picture.
For any $m \ge 3$, we can put $m+2$ vertices on the unit sphere
$$( 0, 0, \pm 1) \quad\text{ and }\quad \left( \cos\frac{2\pi k}{m}, \sin\frac{2\pi k}{m}, 0 \right) \quad\text{ for }\quad 0 \le k < m$$
Their convex hull will be a $m$-gonal bipyramid which appear below.
Up to my knowledge, the largest $n$-vertex polyhedron inside a sphere is known only up to $n = 8$.
- $n = 4$, a tetrahedron.
- $n = 5$, a triangular bipyramid.
- $n = 6$, a octahedron = a square bipyramid
- $n = 7$, a pentagonal bipyramid.
- $n = 8$, it is neither the cube ( volume: $\frac{8}{3\sqrt{3}} \approx 1.53960$ ) nor the hexagonal bipyramid ( volume: $\sqrt{3} \approx 1.73205$ ). Instead, it has volume
$\sqrt{\frac{475+29\sqrt{145}}{250}} \approx 1.815716104224$.
Let $\phi = \cos^{-1}\sqrt{\frac{15+\sqrt{145}}{40}}$, one possible set of vertices are given below:
$$
( \pm \sin3\phi, 0, +\cos3\phi ),\;\; ( \pm\sin\phi, 0,+\cos\phi ),\\
(0, \pm\sin3\phi, -\cos3\phi),\;\; ( 0, \pm\sin\phi, -\cos\phi).
$$
For this set of vertices, the polyhedron is the convex hull of two polylines.
One in $xz$-plane and the other in $yz$-plane. Following is a figure of this polyhedron,
the red/green/blue arrows are the $x/y/z$-axes respectively. The polyhedron has $D_{2}$ symmetry; it may be viewed as a square antiprism modified by buckling the bases along a pair of diagonals.
$\hspace0.75in$ 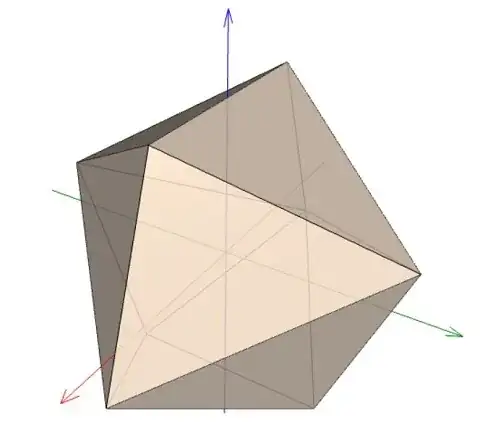
For $n \le 8$, above configurations are known to be optimal. A proof can be found
in the paper
Joel D. Berman, Kit Hanes, Volumes of polyhedra inscribed in the unit sphere in $E^3$
Mathematische Annalen 1970, Volume 188, Issue 1, pp 78-84
An online copy of the paper is viewable at here (you need to scroll to image 84/page 78 at first visit).
For $n \le 130$, a good source of close to optimal configurations can be found
under N.J.A. Sloane's web page on
Maximal Volume Spherical Codes.
It contains the best known configuration at least up to year 1994. For example,
you can find an alternate set of coordinates for the $n = 8$ case from the maxvol3.8
files under the link to library of 3-d arrangements there.
