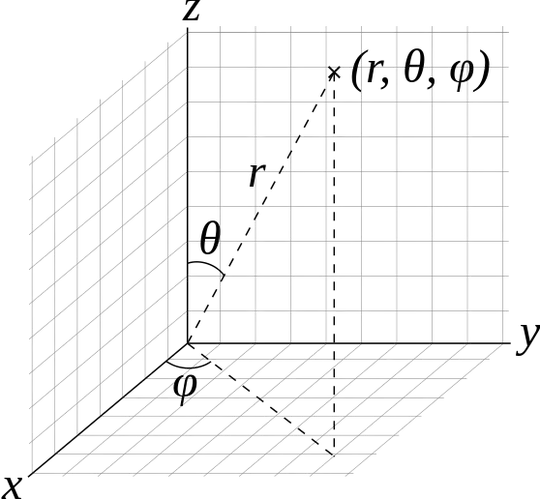
What is the sum of two vectors in spherical coordinates?
The coordinate system:
Assume we have vectors $(r_1,\theta_1,\phi_1)$ and $(r_2,\theta_2,\phi_2)$ in spherical coordinates.
I know the sum vector is not $(r_1+r_2,\theta_1+\theta_2,\phi_1+\phi_2)$ because $\hat r$, $\hat \theta$ and $\hat \phi$ are not fixed like Cartesian coordinates.
but I don't know what the sum vector will be then.
Also I know it is possible to convert to Cartesian and easily sum the components up and get the sum vector. but I want it in spherical system.
In the linked questions, the sum vector is not given in spherical coords. which is what I want.