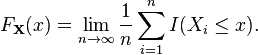Joint distribution of an infinite collection of random variables?

Question

Let's say we have a countable collection of random variables $X_1, X_2, ...$, in $(\Omega, \mathscr{F}, \mathbb{P})$

Can we define a joint distribution function for all of them ie

$$F_{X_1,X_2, ...}(x_1, x_2, ...)?$$

If not, why?

If so, then if the random variables are independent, do we have

$$F_{X_1,X_2,...}(x_1, x_2, ...) = \prod_{i=1}^{\infty} F_{X_i}(x_i)?$$

If the random variables have pdfs or pmfs, do we have

$$f_{X_1,X_2,...}(x_1, x_2, ...) = \prod_{i=1}^{\infty} f_{X_i}(x_i)?$$

---

Edit: Is the empirical distribution function here an example?

---

How about an uncountable collection of random variables $(X_j)_{j \in [0,1]}$?

Can we define $F_{X_j, j \in [0,1]}$?

If the random variables are independent, will product integrals be used?

Answer 1

You can perfectly work with an infinite (countable or not) set of random variables. But you don't do that by defining a "joint distribution function for all of them", that is, a function that takes an infinite number of arguments. That approach would lead you nowhere. For one thing, as suggested by the comment by Did, if we try to define the joint distribution of a countable set of iid variables uniform on $(0,1)$, its value on $x_i=x\in (0,1)$ would be $P(x_i \le x ; \forall i)=\prod_{i=i}^\infty P(x_i \le x)=0 $.

The proper way to characterize the probability law of an infinite set of random variables is by considering the set of distribution functions for every finite subset of those random variables: $F_{X_{i_1},X_{i_2} \cdots X_{i_n}}(x_{i_1},x_{i_2} \cdots x_{i_n})$, for all $n \in \mathbb N$ (finite, of course). Granted, that set of $2^{|\mathcal X|}-1$ distributions must fullfil some consistency conditions (basically, the familiar properties of distribution functions, including marginalization).

That's what is done in the theory of stochastic processes... which are precisely what you are considering: infinite collections (countable or not) of random variables (often indexed by some "time", but that is not essential). The task of dealing with so many distributions is usually less formidable than it seems, because we often impose some restrictions, as stationarity.

The "empirical distribution" you mention has little to do with this. First, it's not a distribution function but a random variable itself. Second, considered as a function of $x$, it's a function of a single variable, not of infinite variables. Informally, it could be regarded as an estimator of the distribution of $X_i$... if the "infinite variables" are iid; but it can also be applied to non-iid variables, to get you some sort of "weighted" distribution function.