Integral of $e^{ix^2}$

Question

How does one evaluate $$\int_{-\infty}^{\infty} e^{ix^2} dx$$

I know the trick how to evaluate $\int_{-\infty}^{\infty} e^{-x^2}dx$ but trying to apply it here I get a limit which does not converge:

$I = \int_{-\infty}^{\infty} e^{ix^2}dx = \int_{-\infty}^{\infty} e^{iy^2}dy \\\implies I^2 = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{i(x^2+y^2)}dxdy = \int_{0}^{2\pi}\int_{0}^{\infty} re^{ir^2} = -\pi i (e^{i\infty}-e^0) $
and $e^{i\infty} $ is not defined.

Are there any other methods? I am not interested in the result (WolframAlpha can do this for me), but rather the method.

Answer 1

All right, let's do some complex analysis! Let's integrate $e^{iz^2}$ over the closed contour defined in three pieces (the arrows indicating the direction of contour integration) $$ \begin{cases} \Gamma_1: & |z|:0\rightarrow R, & \theta=0 \\ \Gamma_2: & |z| = R, & \theta: 0\rightarrow \pi/4\\ \Gamma_3: & |z|:R\rightarrow0, & \theta=\pi/4 \end{cases} $$ which we will eventually want to take the limit $R\rightarrow\infty$.

It can be seen that $$ \int_0^\infty e^{ix^2}dx=\lim\limits_{R\rightarrow\infty}\int_{\Gamma_1}e^{iz^2}dz $$ and since $e^{ix^2}$ is an even function $$ \int_{-\infty}^{\infty}e^{ix^2}dx=2\int_0^\infty e^{ix^2}dx $$ so we're heading in the right direction.

Now Cauchy's Theorem states that $$ \oint_D f(z)dz =0 $$ for $f(z)$ analytic in $D$. Our function, $e^{iz^2}$, has no singularities and is defined on the entire complex plane, so it is considered an entire function, and Cauchy's Theorem holds for our closed contour: $$ \int_0^R e^{ix^2}dx+\int_{\Gamma_2}e^{iz^2}dz+\int_{\Gamma_3}e^{iz^2}dz=0 $$

For our second integral above, we show that it vanishes as $R\rightarrow\infty$ using the ML test given by $$ \left|\int_\Gamma f(z)dz\right|\leq ML $$ where $M$ is a finite upper bound of $f(z)$ and $L$ is the length of the contour $\Gamma$. Of course, we need to assume that $f(z)$ is bounded and analytic on $\Gamma$ for this. In order to apply the ML test, we substitute into our integrand $z=re^{i\theta}$ so that $$ z^2 = r^2e^{2i\theta} = r^2\cos(2\theta)+ir^2\sin(2\theta) $$ $$ |e^{iz^2}|=|e^{ir^2\cos(2\theta)-r^2\sin(2\theta)}|\leq e^{-R^2}=M $$ because $r=R$ on this contour and $\sin(2\theta)\leq1$. While, $$ L=\frac{\pi R}{4} $$ since we are looking at $1/8$th of the perimeter of the circle with radius $R$. By the ML test $$ \left|\int_{\Gamma_2} e^{iz^2}dz\right| \leq e^{-R^2}\frac{\pi R}{4} $$ which goes to $0$ as $R\rightarrow\infty$.

Now we want to deal with the 3rd contour integral $\Gamma_3$. Fortunately, the contour we picked allows us to easily parameterize this integral, as $y=x$. We will also need $z^2=(x+iy)^2=x^2-y^2+2ixy$. Recalling that $dz=dx+idy$ the integral becomes $$ \int_{\Gamma_3} e^{i(x^2-y^2)-2xy}(dx+idy) =\int_{R}^{0} e^{-2x^2}dx+i\int_{R}^{0} e^{-2y^2}dy \rightarrow-\sqrt{\frac{\pi}{8}}(1+i)\ \text{as}\ R\rightarrow0 $$ from our real Gaussian integral identities.

Taking $R\rightarrow\infty$, our results for the contour integrals in our Cauchy's Theorem equation imply that $$ \int_0^\infty e^{ix^2}dx = \sqrt{\frac{\pi}{8}}(1+i) $$

The integral from $-\infty$ to $\infty$ is just twice this. So boom.

If you want, you can rewrite $e^{ix^2}=\cos(x^2)+i\sin(x^2)$ and equate the real and imaginary parts in the last equation and you will get the limiting values of the Fresnel Integrals.

Boom.

Also, since $$ (1+i)=\sqrt{2}e^{i\pi/4}=\sqrt{2e^{i\pi/2}}=\sqrt{2i} $$ we have $$ \int_0^\infty e^{ix^2}dx = \sqrt{\frac{i\pi}{4}} = \frac{1}{2}\sqrt{-\frac{\pi}{i}} $$

which exactly matches the well-known Gaussian integral identity $$ \int_0^\infty e^{-\alpha x^2}dx = \frac{1}{2}\sqrt{\frac{\pi}{\alpha}} $$ with $\alpha=-i$. Boom. Thus, this suggests that this identity can work for imaginary $\alpha$, and possibly certain complex $\alpha$ with the right combination of real and imaginary parts as well as choice of contours that do not make our integrals blow up.

Answer 2

This answer is dedicated to give an alternative proof of

$$ \lim_{R\to+\infty}\int_\Gamma e^{iz^2}\mathrm dz=0 $$

where $\Gamma$ denotes a circular arc connecting $R$ and $e^{i\pi/4}R$. Using the parametrization that $z=Re^{i\theta}$, we have

\begin{aligned} \left|\int_\Gamma e^{iz^2}\mathrm dz\right| &\le R\int_0^{\pi/4}e^{-R^2\sin(2\theta)}\mathrm d\theta \\ &=R\left(\int_0^\delta+\int_\delta^{\pi/4}\right)e^{-R^2\sin(2\theta)}\mathrm d\theta \\ &<R\delta+{R\pi\over4}e^{-R^2\sin(2\delta)} \end{aligned}

Since $\sin u\sim u$ when $u\to0$, we see that for small $\delta>0$ there is $\sin(2\delta)>\delta$, which means when $\delta=R^{-3/2}$ and $R$ is large there is

$$ \left|\int_\Gamma e^{iz^2}\mathrm dz\right|<{1\over\sqrt R}+{\pi R\over2}e^{-\sqrt R}=O\left(1\over\sqrt R\right) $$

Answer 3

Here is another solution with a different contour.

Let $$I=\int^{\infty}_{-\infty}e^{ix^2}\text{ d}x$$ and let $$f(z)=e^{iz^2}$$ Note that our function is even.

In user279043's answer, the contour they chose was (what I would presume) based on the fact that the complex integrand can be rewritten like this $$\exp\left(z^2e^{\frac{i\pi}2}\right)=\exp\left(\left(ze^{\frac{i\pi}4}\right)^2\right)$$ which implies that the integrand is well behaved along the ray $e^{\frac{i\pi}4}$.

However, we can also note that along the imaginary axis, our function is similarly well behaved. Consider the following contour shown below

consisting of the paths $$\mathcal{C}=B+\Gamma+L$$ Thus, our contour integral about said contour would be $$\oint_{\mathcal{C}}f(z)\text{ d}z=\int_B+\int_{\Gamma}+\int_Lf(z)\text{ d}z=0$$ Each path can be parameterized as follows \begin{alignat*}{5} B&:\text{ }z=x,\qquad &\text{d}z&=\text{d}x,\qquad &x&\in[0, R\,]\\ \Gamma &:\text{ }z=Re^{i\theta},\qquad &\text{d}z&=iRe^{i\theta}\text{ d}\theta,\qquad &\theta&\in\left[0, \frac{\pi}{2}\right]\\ L&:\text{ }z=iy,\qquad &\text{d}z&=i\text{d}y,\qquad &y&\in[\,R, 0] \end{alignat*} Now let's evaluate each integral. The integral about $B$ is just half of $I$ $$\lim_{R\to+\infty}\int_Bf(z)\text{ d}z=\lim_{R\to+\infty}\int^{R}_0e^{ix^2}\text{ d}x=\frac{1}{2}I$$ The integral about $\Gamma$ vanishes along our integration interval using typical inequalities. Note that I put in red whatever goes to $1$. \begin{align} \left|\int_{\Gamma}f(z)\text{ d}z\right|&\le\int^{\frac{\pi}2}_{0}\left|e^{iR^2e^{2i\theta}}\right|\cdot\color{red}{|i|}|R|\color{red}{\left|e^{i\theta}\right|}\text{ d}\theta\\ &\le\int^{\frac{\pi}2}_{0}R\color{red}{\left|e^{iR^2\cos(2\theta)}\right|} \left|e^{-R^2\sin(2\theta)}\right| \text{ d}\theta\\ &\le\int^{\frac{\pi}4}_{0}R e^{-R^2\cdot \frac{4\theta}{\pi}} \text{ d}\theta+\int^{\frac{\pi}2}_{\frac{\pi}4}R e^{R^2\cdot \frac{4\left(\theta-\frac{\pi}{2}\right)}{\pi}} \text{ d}\theta \end{align} Which goes to $0$ when we take the limit as $R$ goes to infinity. The third line comes from Jordan's inequality.

Lastly, the integral along $L$ gives $$\lim_{R\to+\infty}\int_Lf(z)\text{ d}z=\lim_{R\to+\infty}\int^{0}_{R}e^{i(iy)^2}\cdot i\text{ d}y=-i\int^{\infty}_0e^{-iy^2}\text{ d}y$$ So we have $$\oint_{\mathcal{C}}f(z)\text{ d}z=\int_B+\int_{\Gamma}+\int_Lf(z)\text{ d}z=\frac12 I-i\int^{\infty}_0e^{-iy^2}\text{ d}y=0$$ Lastly, we can rearrange our equation and solve as follows \begin{align} \frac12 I&=i\int^{\infty}_0e^{-iy^2}\text{ d}y\\ \implies\left(\frac{I}{2i}\right)^2&=\int^{\infty}_0e^{-iy^2}\text{ d}y\cdot\int^{\infty}_0e^{-it^2}\text{ d}t\\ &=\int^{\infty}_0\int^{\infty}_0e^{-i(y^2+t^2)}\text{ d}y\text{ d}t\\ &=\int^{\frac{\pi}2}_0\int_0^{\infty}e^{-ir^2}\cdot r\text{ d}r\text{ d}\theta=\frac{\pi}{2}\int_0^{\infty}re^{-ir^2}\text{ d}r\\ &=\frac{\pi}{4i}\int^{\infty}_0e^{-u}\text{ d}u=\frac{\pi}{4i}\cdot 1\\ \implies \frac{I}{2i}&=\sqrt{\frac{\pi}{4i}}\\ \implies I&=2i\cdot\frac{\sqrt{\pi}}{2}\cdot e^{-\frac{i\pi}{4}}=\sqrt{\pi}e^{\frac{i\pi}4}=(1+i)\sqrt{\frac{\pi}{2}} \end{align} we can see that line 4 follows from the polar coordinate change of variables $$y=r\cos(\theta),\,\,t=r\sin(\theta),\qquad J_f=\left[\begin{array}{cc} \cos(\theta)& -r\sin(\theta) \\ \sin(\theta)& r\cos(\theta) \end{array}\right],\qquad \left|\det\left(J_f\right)\right|=r$$ and line 5 follows from this simple u-sub $$u= ir^2,\qquad\frac{\text{d}u}{\text{d}r}=2ir,\qquad\text{d}r=\frac{\text{d}u}{2ir}$$

Hence $$I=\boxed{(1+i)\sqrt{\frac{\pi}{2}}}$$

Answer 4

Another method.

$$\int_{-\infty}^\infty\exp(ix^2)\mathrm dx=2\int_0^{\infty} \exp(ix^2)\mathrm dx\tag{1}$$

Let $-z=ix^2\implies x=(iz)^{1/2}\implies \mathrm dx=\frac{i^{1/2}}{2}z^{-1/2}\mathrm dz$ hence $$\int_0^{\infty} \exp(ix^2)\mathrm dx=\frac{i^{1/2}}{2}\int_0^{-i\infty}z^{-1/2}\exp(-z)\mathrm dz\tag{2}$$

This is almost the Gamma function, but the limits of integration are wrong. We need to somehow argue that we can switch the $\int_0^{-i\infty}$ to $\int_0^\infty$. We consider the following contour in the complex plane:

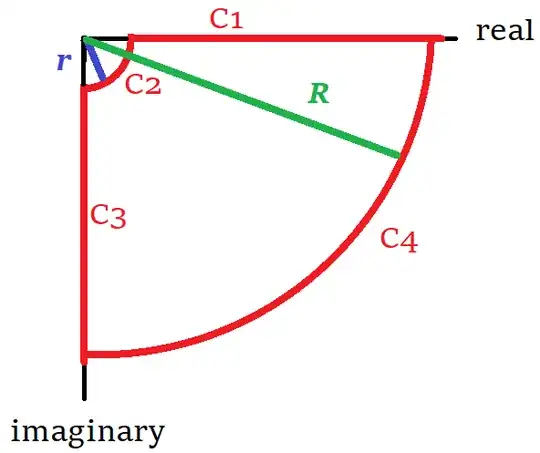
We call this closed contour $C(r,R)$, a union of the four curves $C_1,C_2,C_3,C_4~(r,R)$. Explicitly, $$C_1(r,R)=\{t\mid t\in[R,r]\} \\ C_2(r)=\{re^{it}\mid t\in[0,-\pi/2]\} \\ C_3(r,R)=\{-it\mid t\in[r,R]\} \\ C_4(R)=\{Re^{it}\mid t\in[3\pi/2,2\pi]\} \\ C(r,R)=C_1(r,R)\cup C_2(r)\cup C_3(r,R)\cup C_4(R)$$

Because we have an integrand that is analytic everywhere in the interior and on the boundary of $C(r,R)$, we know that $$\oint\limits_{C(r,R)}z^{-1/2}\exp(-z)\mathrm dz=0$$

Obviously, what we'd like to show is that the integrals on $C_2$ and $C_4$ go to $0$ as $r\to 0,R\to\infty$. Let's have a look at $C_2$ first. Being that the integration goes in the counter-clockwise direction, we actually traverse $C_2$ in the clockwise direction and so we can parameterize the integration along $C_2$ as $$\int\limits_{C_2(r)}z^{-1/2}\exp(-z)\mathrm dz=\int_{0}^{-\pi/2}(re^{it})^{-1/2}\exp(-re^{it})ire^{it}\mathrm dt$$

Simplifying things a little, $$\int\limits_{C_2(r)}z^{-1/2}\exp(-z)\mathrm dz=-ir^{1/2}\int_{0}^{\pi/2}e^{it/2}\exp(-re^{-it})\mathrm dt$$

As $r\to 0$ we use a Taylor expansion on the $\exp$: $$\exp(-re^{-it})=1-re^{-it}+\mathrm O(r^2)$$

So $$\int\limits_{C_2(r)}z^{-1/2}\exp(-z)\mathrm dz=-ir^{1/2}\int_{0}^{\pi/2}e^{it/2}\exp(-re^{-it})\mathrm dt \\ =-ir^{1/2}\int_0^{\pi/2}e^{it/2}\mathrm dt+ir^{1/2}\int_0^{\pi/2}e^{it/2}re^{it}\mathrm dt +\mathrm O(r^2)\\ =ir^{1/2}\cdot(\text{integral not depending on}~r)+ir^{3/2}\cdot(\text{integral not depending on}~r)+\mathrm O(r^2) \\ =\mathrm O(r^{1/2})\to 0~\text{as}~r\to 0.$$

Now we look at $C_4$. This path is indeed counter-clockwise so we parameterize as such: $$\int\limits_{C_4(R)}z^{-1/2}\exp(-z)\mathrm dz=\int_{3\pi/2}^{2\pi}(Re^{it})^{-1/2}\exp(-Re^{it})iRe^{it}\mathrm dt \\ =iR^{1/2}\int_{3\pi/2}^{2\pi}e^{it/2}\exp(-Re^{it})\mathrm dt$$

Expanding with Euler's formula, $$\int\limits_{C_4(R)}z^{-1/2}\exp(-z)\mathrm dz=iR^{1/2}\int_{3\pi/2}^{2\pi} e^{it/2}\exp(-R\cos t-iR\sin t)\mathrm dt \\ =iR^{1/2}\int_{3\pi/2}^{2\pi} e^{it/2}\exp(-R\cos t)\exp(-iR\sin t)\mathrm dt $$

We know that $|\exp(-iR\sin t)|=|e^{it/2}|=1$ and so via the estimation lemma we know that $$\left|\int_{C_4(R)}z^{-1/2}\exp(-z)\mathrm dz\right|= R^{1/2}\left|\int_{3\pi/2}^{2\pi} e^{it/2}\exp(-R\cos t)\exp(-iR\sin t)\mathrm dt\right| \\ \leq R^{1/2}\left|\int_{3\pi/2}^{2\pi}\exp(-R\cos t)\mathrm dt\right|\tag{3}$$

Past this point, the simple bound from the estimation lemma is actually not enough here, as it would only give us $$\left|\int_{C_4(R)}z^{-1/2}\exp(-z)\mathrm dz\right|\leq \frac{\pi}{2}R^{1/2}$$

Which still goes to $\infty$ as $R\to \infty$. So we need to find a better way to bound the integral $\int_{3\pi/2}^{2\pi}\exp(-R\cos t)\mathrm dt$. Due to periodicity, $$\int_{3\pi/2}^{2\pi}\exp(-R\cos t)\mathrm dt=\int_{-\pi/2}^{0}\exp(-R\cos t)\mathrm dt$$

And then the evenness of the integrand,
$$\int_{-\pi/2}^{0}\exp(-R\cos t)\mathrm dt=\int_0^{\pi/2}\exp(-R\cos t)\mathrm dt$$

Here we will need to consult some mathematical literature. It turns out that $$\int_0^{\pi/2}\exp(-R\cos t)\mathrm dt=-\frac{\pi}{2}M_0(R)$$

Where $M_0$ is a zeroth-order Modified Struve function. It has the asymptotic expansion $$M_0(z)\asymp\frac{-1}{2\pi z}+\mathrm O(|z|^{-2}) \\ \text{as}~|z|\to\infty\\ (\operatorname{Re}z>0)$$ Which means, going back to $(3)$, $$\left|\int_{C_4(R)}z^{-1/2}\exp(-z)\mathrm dz\right|\leq R^{1/2}\frac{\pi}{2}M_0(R)\asymp \frac{1}{4R^{1/2}}$$ Which allows us to conclude $$\left|\int_{C_4(R)}z^{-1/2}\exp(-z)\mathrm dz\right|\to 0 \\ \text{as}~R\to\infty$$

Therefore, $$0=\oint_{C(r,R)}z^{-1/2}\exp(-z)\mathrm dz =\left(\int\limits_{C_1(r,R)}+\int\limits_{C_2(r)}+\int\limits_{C_3(r,R)}+\int\limits_{C_4(R)}\right)z^{-1/2}\exp(-z)\mathrm dz \\ \to \left(\int\limits_{C_1(r,R)}+\int\limits_{C_3(r,R)}\right)z^{-1/2}\exp(-z)\mathrm dz~~\text{as}~r\to 0~,~R\to\infty$$ This finally allows us to conclude $$\int_0^{-i\infty}z^{-1/2}\exp(-z)\mathrm dz=-\int_\infty^0 z^{-1/2}\exp(-z)\mathrm dz \\ =\int_0^\infty z^{1/2-1}\exp(-z)\mathrm dz \\ =\Gamma(1/2)=\sqrt{\pi}$$ Going all the way back to the beginning, this means $$\int_{-\infty}^\infty\exp(ix^2)\mathrm dx=i^{1/2}\sqrt{\pi}=\sqrt{\frac{\pi}{2}}+i\sqrt{\frac{\pi}{2}}$$ Which instantly gives us the famous Fresnel Integrals: $$\boxed{\int_{-\infty}^\infty \cos(x^2)\mathrm dx=\int_{-\infty}^\infty \sin(x^2)\mathrm dx=\sqrt{\frac{\pi}{2}}}$$

---

While lengthier than the other responses, this answer is, in my opinion, far more direct than the others and I think is an accurate reflection of the calculations one would have to go through if one had not seen the problem beforehand. It's my first full attempt at solving this problem, anyhow.