We'd like to calculate the integral
$$\int_{0}^\infty t^{n}\exp(-z^2t^2)\mathrm dt\tag{1}$$
Note that it converges only when $\operatorname{Re}(z^2)>0$.
And what we've done is introduce the new variable $s=zt$ which changes it to
$$\int_{0}^{\infty}t^{n}\exp(-z^2t^2)\mathrm dt=\frac{1}{z^{n+1}}\int_{0}^{z\infty}s^{n}\exp(-s^2)\mathrm ds$$
And we'd like to prove that we can rotate the path of integration without any issues, i.e
$$\frac{1}{z^{n+1}}\int_0^{z\infty}s^{n}\exp(-s^2)\mathrm ds=\frac{1}{z^{n+1}}\int_0^{\infty}s^{n}\exp(-s^2)\mathrm ds\tag{2}$$
I carry out an almost identical calculation here though this case is actually easier because there is no singularity at the origin. We consider a sector in the complex plane:
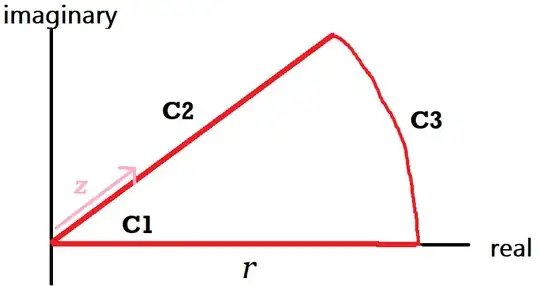
We denote this sector by $C(r)$. Explicitly,
$$C_1(r)=\{t\mid t\in[0,r]\} \\ C_2(z,r)=\{r\mathrm e^{\mathrm it}\mid t\in[0,\operatorname{arg}z]\} \\ C_3(z,r)=\{zt\mid t\in[r,0]\} \\ C(z,r)=C_1(r)\cup C_2(z,r)\cup C_3(z,r)$$
Obviously my diagram assumes $\operatorname{Re}z,\operatorname{Im}z>0$ but this calculation is easily repeatable in any of the four quadrants. We know, because we are dealing with an integrand that is analytic everywhere on and in the contour, that
$$0=\oint_{C(z,r)}s^{n}\exp(-s^2)\mathrm ds=\left(\int_{C_1(r)}+\int_{C_2(z,r)}+\int_{C_3(z,r)}\right)s^{n}\exp(-s^2)\mathrm ds$$
Now, obviously what we'd like to show is that $\int_{C_3(z,r)}s^n\exp(-s^2)\mathrm ds\to 0$ as $r\to\infty$. This is actually quite tedious. First see that
$$\int_{C_3(z,r)}s^{n}\exp(-s^2)\mathrm ds=\int_{0}^{\operatorname{arg}z}r^n\mathrm e^{\mathrm int}\exp(-r^2\mathrm e^{2\mathrm it})~\mathrm ir\mathrm e^{\mathrm it}\mathrm dt$$
By the estimation lemma,
$$\left|\int_{0}^{\operatorname{arg}z}r^n\mathrm e^{\mathrm int}\exp(-r^2\mathrm e^{2it})~\mathrm ir\mathrm e^{\mathrm it}\mathrm dt\right|\leq \int_{0}^{\operatorname{arg}z}\left|r^{n+1}\exp(-r^2\mathrm e^{2\mathrm it})\right|\mathrm dt$$
Then,
$$\left|r^{n+1}\exp(-r^2\mathrm e^{2\mathrm it})\right|=r^{n+1}\bigg|\exp\big(-r^2(\cos(2t)+\mathrm i\sin(2t))\big)\bigg| \\ =r^{n+1}\bigg|\exp(-r^2\cos(2t))\bigg|$$
Which allows us to deduce (via a simple change of variable $2t\to t$)
$$\left|\int_{C_3(z,r)}s^{n}\exp(-s^2)\mathrm ds\right|\leq \frac{1}{2}r^{n+1}\int_{0}^{2\operatorname{arg}z}\exp(-r^2\cos t)\mathrm dt$$
At this point, things become a little tricky. Note that
$$\operatorname{Re}(z^2)>0\implies\begin{matrix}|\operatorname{arg}z|<\pi /4 \\ \text{or}\\|\operatorname{arg}(-\overline{z})|<\pi/4\end{matrix}$$
I will focus on the right half plane, i.e $|\operatorname{arg}z|<\pi /4$. (Again, this calculation is easily repeatable for the other side of the plane.) From this we know that $2\operatorname{arg}z\in (-\pi/2,\pi/2)$. This allows us to deduce that $\exp(-r\cos(t))$ is increasing for $t\in[0,2\operatorname{arg} z]$. Letting $2\operatorname{arg} z=\phi$ for short this allows us to bound
$$\left|\int_{C_3(z,r)}s^{n}\exp(-s^2)\mathrm ds\right|\leq \frac{1}{2}r^{n+1}\int_{0}^{\phi}\exp(-r^2\cos t)\mathrm dt\leq \frac{r^{n+1}}{2}\int_{0}^{\phi}\exp(- r^2\cos \phi)\mathrm dt$$
So
$$\left|\int_{C_3(z,r)}s^{n}\exp(-s^2)\mathrm ds\right|\leq \frac{\phi}{2}r^{n+1}\exp(- r^2\cos \phi)$$
Which clearly goes to $0$ as $r\to\infty$, as $\cos \phi>0$. It is not so easy in my linked post because in that case we had $\phi=\pi/2$.
Now, for the finishing touches. We can see that
$$\int_{0}^{z\infty} s^n\exp(-s^2)\mathrm ds=\lim_{r\to\infty}\int_{C_2(z,r)}s^n\exp(-s^2)\mathrm ds$$
And, our above argument shows that $\int_{C_2}\to\int_{C_1}$ as $r\to \infty$ hence
$$\int_0^{z\infty}s^n\exp(-s^2)\mathrm ds=\int_0^{\infty}s^n\exp(-s^2)\mathrm ds$$
This integral is easy to calculate using the Gamma function. It is also easy to see that this can be extended to complex values of $n$ which allows us to finally write (substituting $z^2\to z$ and $n\to \nu-1$)
$$\boxed{\int_0^\infty t^{\nu-1}\exp(-zt^2)=\frac{1}{2z^{\nu/2}}\Gamma\left(\frac{\nu}{2}\right) \\ \text{for}~\big(\operatorname{Re}(z)>0~\text{and}~\operatorname{Re}(\nu)>0\big)}$$
