2

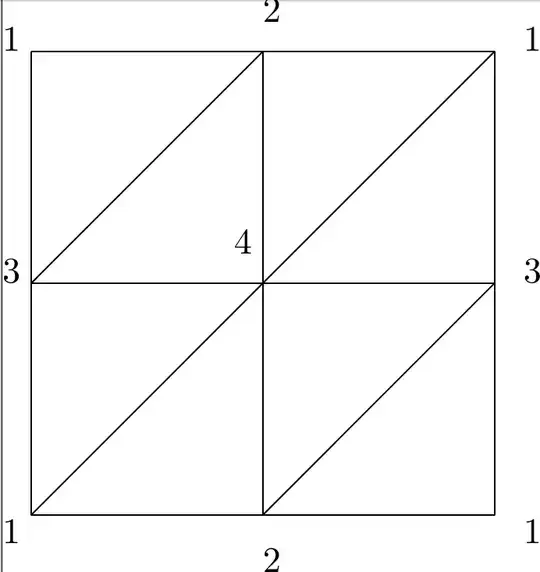
On page 133 of Rotman's Introduction to Algebraic Topology it is stated that one requires at least 14 triangles in any triangulation of the torus.

Admittedly, I do not have a very good understanding of triangulations.

From what I understand, the following seems like a perfectly valid triangulation of the torus:

Figure

What is the mistake in this?

Soheil Haghighi
  • 73
  • 6
caffeinemachine
  • 19,646
  • The 123 and 341 triangles on the left have separate edges (the vertical lines on the left) that share both end points 1 and 3. IIRC that is not allowed in a simplicial complex. – Jyrki Lahtonen Aug 23 '15 at 17:04

1 Answers1

6

The NE and SW blocks both contain triangles with vertices 1,3,4. But these intersect in just the edge 13 and the vertex 4, while the intersection of two simplices in a triangulation must be a "face" of each (which might be the empty simplex), not a union of two or more simplices.

John Hughes
  • 100,827
  • 4
  • 86
  • 159