4

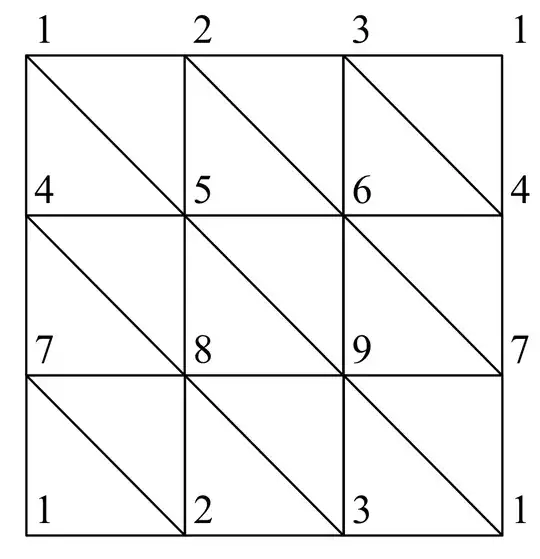
On pg. 133 of Rotman's Introduction to Algebraic Topology, we have a figure enter image description here

which claims to be a triangulation of the torus.

Now a triangulation of a topological space is defined as

Definition. A triangulation of a topological space $X$ is a finite simplicial complex $K$ (in some Euclidean space) along with a homeomorphism $h:|K|\to X$.

I interpret the picture as a simplicial complex $K$ whose members are each of the little triangles along with all their edges and vertices. To claim that the given figure is a triangulation, we need to produce a homeomorphism $h:|K|\to T$, where $T$ denotes the torus.

One way to give a map from $|K|$ to $T$ is by seeing $T$ as the quotient space formed by identifying the left and the right edges and the top and the bottom edges (the usual way of making a torus from a rectangular piece of paper), and having the map $h:|K|\to T$ as the quotient map.

But this quotient map is not a homeomorphism since it is not a bijection.

I must be missing something obvius.

Michael Hardy
  • 1
caffeinemachine
  • 19,646

1 Answers1

4

Here on this picture some simplexes are identified. When you give names to different vertices, it will look as follows enter image description here

Michael Hardy
  • 1
Andrey Ryabichev
  • 2,810
  • The diagram suggests the same kind of identification I had mentioned in the OP. The quotient space under the identification is the torus. My problem is that I cannot imagine a simplicial complex whose underlying space is homoeomorphic to the torus. Can you please address this? Thanks. – caffeinemachine Aug 23 '15 at 14:52
  • @caffeinemachine, there are eight (abstract) vertices $1,2,\dots9$, twenty seven edges $(12), (13), (14), (15), (17), (19)$, $(23), (25), (26), (27), (28)$... and eighteen triangles $(125),(139), (145)$..... – Andrey Ryabichev Aug 23 '15 at 15:04
  • Oh. So this diagram is actually representing an abstract simplicial complex rather than a (geometric) simplicial complex. And we have a theorem which says that any abstract simplicial complex admits a geometric realization. Is this what is going on here? – caffeinemachine Aug 23 '15 at 15:24
  • @caffeinemachine, yes, and geometric realization is that we can define, this is not a theorem – Andrey Ryabichev Aug 23 '15 at 15:28