12

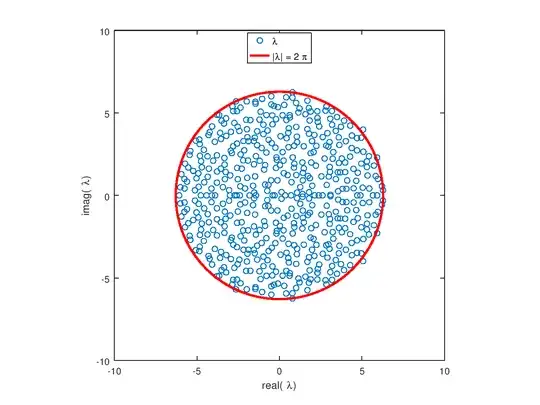
I just investigated randn(1024) + 1i*randn(1024), a 1024x1024 complex valued matrix with elements both real part and imaginary part drawn from $\mathcal{N}(\mu = 0, \sigma = 1)$. I was a bit surprised when I found that the eigenvalue distribution seemed to be uniformly distributed over a circular disc in the complex plane. I.e. constant density of eigenvalues within the circle.

As I have studied some matrix perturbations, I was thinking that every new random addition performs a random walk on each eigenvalue. But if that was the case, it would seem more likely that the probability to reach points far out on the disc should drop, but that does not happen.

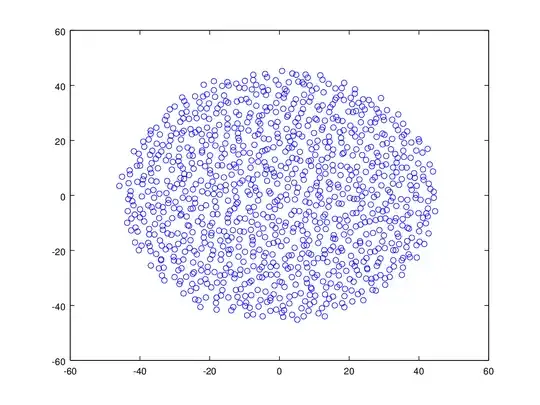
enter image description here

Does anyone know any good way to analyze or explain this?

Edit I did another command

In other words: $$A \text{ is } 512\times 512 \hspace{1cm}{\bf A}_{ij} = \frac{\mathcal{N}(0,2\pi)}{\sqrt{512}}, \forall (i,j)$$

A = 2*pi*(randn(512))/sqrt(512);

Now it seems I can get the picture below, all within $2\pi$:

enter image description here

mathreadler
  • 26,534
  • This is basically Girko's law for complex matrices. The original law is for real random matrices. http://mathworld.wolfram.com/GirkosCircularLaw.html – Alex R. Jul 03 '15 at 23:32
  • Ok, nice to know it has it's own name, but has anyone found an explanation? – mathreadler Jul 04 '15 at 00:04
  • 3
    @mathreader: It's a theorem due to Girko and Bai for normal random variables, and was extended by Tao and Vu for more general random variables. See here for example: https://terrytao.wordpress.com/2007/08/23/random-matrices-the-circular-law/ The theorem is not trivial to prove. – Alex R. Jul 04 '15 at 01:13
  • Ok great, thank you Alex. He has a parenthesis error on $\mu_\infty(s,t)$, though – mathreadler Jul 04 '15 at 10:08

0 Answers0