Plot the eigenvalues of many $n\times n$ real matrices in the complex plane, where the matrices are taken from a some distribution. For $n>7$, you can start to see a hole at the origin starting to form. From Girko's Circular Law I'd expect the distribution to tend toward a solid disc (with no hole in it). Below, the eigenvalue distributions of $10\times 10$ matrices taken from three distributions are seen, all with holes in them. The bigger $n$ is, the larger the hole is. The distributions are:
- All entries of all matrices are $\mathcal{N}(0,1)$
- All entries of all matrices are $\mathcal{U}(0,1)$
- The matrices are picked uniformly over the volume of a unit $n^2$-ball.
Is this real (and not a bug in my code)? If it is, what is this phenomenon called?
This seems to violate Girko's Circular Law, so what am I missing?
Edit: Here is my Matlab-code for generating these (without the scatterplot):
n = 10;
X = zeros(10^5,1);
Y = zeros(10^5,1);
for i = 1:10^5
B = randn(n);
C = eig(B);
j = 1+4*(i-1);
X(j:j+n-1) = real(C);
Y(j:j+n-1) = imag(C);
end
Have I perhaps made some stupid mistake?
2nd edit: Here is a plot with the corrected code, as requested: 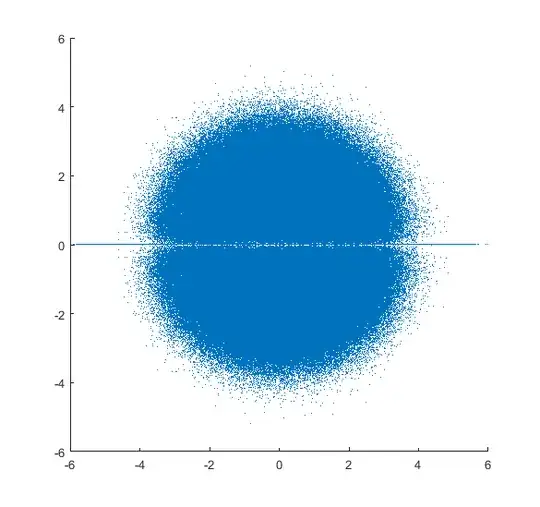

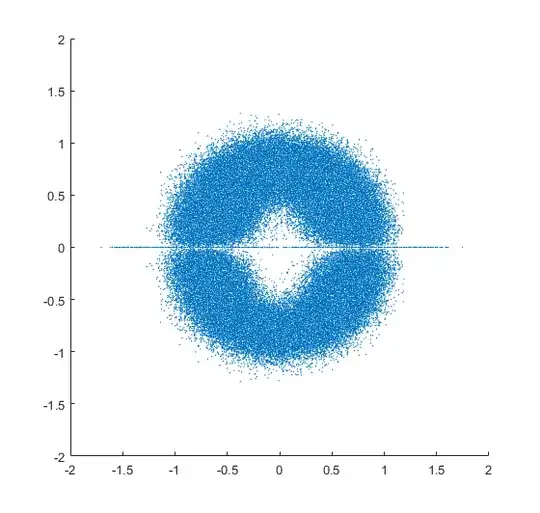
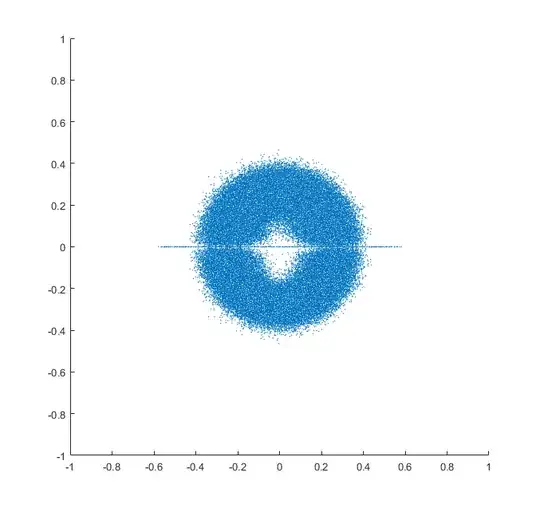

randn(n),rand(n)and so on. I would think that that would be sufficient, but perhaps not? – Bobson Dugnutt May 19 '17 at 17:27randn(): "the default datatype is 'double'." I implemented it anyway, and it didn't change anything. – Bobson Dugnutt May 19 '17 at 17:42