5

Maybe this is an idiot question and I'm committing a trivial mistake. Let $\phi (\theta, \varphi) = (\cos \theta \sin \varphi, \sin \theta\sin \varphi, \cos \varphi)$ be the usual covering of the circle $\mathbb{S}^2 (1)$ by spherical coordinates

I always thought that polar coordinates could be seen as the picture, for instance, in here http://en.wikipedia.org/wiki/Spherical_coordinate_system (second picture). In this case it would be a covering space map.

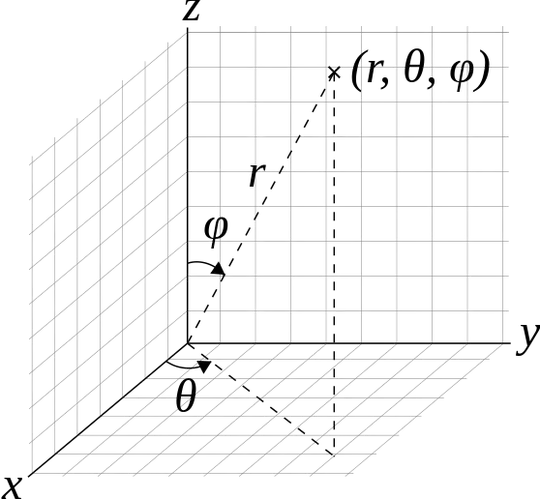
enter image description here

However when $\theta = 0$, the coordinates satisfies $(\sin \varphi, 0, \cos \varphi)$, which is a circle in the plane $y = 0$, but the angle $\theta$ is $0$ and $(-1, 0, 0)$ belongs to circle! However according to the image in the link $\theta$ should be $\pi$. So $\phi (0 \times (0, 2\pi)) \cap \phi (\pi \times (0, 2\pi)) \neq \emptyset$. Therefore I'm now not sure if $\phi$ is a covering space.

So, is $\phi$ a covering space map? And what's wrong with that $\theta$?

Rephrasing my question into one: in squares of what size $\phi$ is injective?

Thanks in advance.

EDIT

I've just realized that the map $\phi$ cannot be a covering. Since $\mathbb{S}^2(1)$ is already simply connected, $\mathbb{R}^2$ cannot be a covering space, otherwise it would be the universal covering.

Let $U_{a, b} = (a, 2\pi + a)\times(b, \pi + b)$. The function $\phi|_{U_{a, b}}$ is not an injection unless $a, b \in \mathbb{Z}$ (as noted by user86418). As discussed in the comments, I (and I think the other commenters) thought that $\mathbb{R}^2$ could be tessellated by the rectangles $U_{i, j}$ where $i, j \in \mathbb{Z}$. However this is not true, since this tessellation would not be induced by a group $G$ (otherwise $G \cong \pi_1 (\mathbb{S}^2) = 0$)

By making a more detailed analysis, it's possible to see that in the rectangle $R_{0,0} = \overline{U_{0, 0}}$, a vertical arrow pointing down is equivalent to an arrow pointing up (with the source) translated by $(\pi, 2\pi)$. More precisely, a point $(\theta, \varphi)$ is identified with a point $(\theta + \pi, 2\pi - \varphi)$. Together with this "action", there is the usual identification beetween $(\theta, \varphi)$ and $(\theta + k2\pi, \varphi + l2\pi)$.

In this case, the second action is given by $\mathbb{Z}^2$ (by translating by $2\pi$) and, in the quotient $X \cong \mathbb{R}^2/ \mathbb{Z}^2$, the first "action" turns in to a real action given by $\mathbb{Z}_2$. Therefore $\mathbb{S}^2 \cong X /\mathbb{Z}^2$. But, since $X \cong \mathbb{T}^2$ is a torus, this would imply that the sphere is a quotient of a torus by $\mathbb{Z}^2$. Is this correct?

So summarizing, the action on the torus by the additive group $\mathbb{Z}^2$ is given by $1. (\theta, \varphi) = (\theta + \pi, 2\pi - \varphi)$.

So the questions are:Is $\mathbb{S}^2 \cong \mathbb{T}^2/ \mathbb{Z}^2$ as descripted above? Furthermore, for what open set $\phi$ fails to be a covering (i.e, when $\phi^{-1} (U)$ fails to be a disjoint union of isomorphic open sets)?

user40276
  • 5,543
  • I'm not sure if it's what causes trouble to you, but a covering map needs not be bijective, it has only to be surjective. Maybe have a look at covering space on Wikipedia. – Jean-Claude Arbaut Jun 01 '15 at 07:46
  • @jca Thanks, but I know this. The problem is that I though that this covering would give a tessellation of the plane into squares of size $2\pi$, however apparently this is not true. – user40276 Jun 01 '15 at 08:06
  • "Length" $2\pi$ on the $\theta$ side, but $\pi$ on the $\varphi$ side. – Jean-Claude Arbaut Jun 01 '15 at 08:14
  • 1
    @user40276 If you want to have non-overlapping intervalls, you should define more strictly the ranges of $(\theta,\varphi)$. For instance $[0,2\pi]\times[0,\pi]$ – Martigan Jun 01 '15 at 08:14
  • @Martigan So do you mean that on each square, $(a, 2\pi + a)\times (b, 2\pi + b)$, $\phi$ is injective? – user40276 Jun 01 '15 at 08:41
  • @Martigan It's the idea, but it won't work as is, because for example with $\varphi \in (\pi/2, \pi/2+\pi)$, you don't get a bijection : it's neither injective nor surjective. – Jean-Claude Arbaut Jun 01 '15 at 08:48
  • @user40276 No, for two reasons : one, it is too large ($2\pi$ for the $\varphi$ is too much). Second, this does not work for any intervall like this, for by restricting the range of $\varphi$, this is linked with range of $\theta$. You need to cover $[0,\pi]$ with $\varphi$. – Martigan Jun 01 '15 at 08:48
  • @jca: agreed. I specified $[0,\pi]$ for this reason. – Martigan Jun 01 '15 at 08:50
  • @Martigan Sorry I mistyped, I mean $(a, 2\pi + a)\times(b , \pi + b)$. – user40276 Jun 01 '15 at 08:52

3 Answers3

6

No matter how you slice it (mathematicians' or physicists' conventions; latitude or colatitude, etc., etc.), spherical coordinates fail to be a covering map near the "poles", usually the points on the $z$-axis, where every longitude corresponds to a single point. (What time zone does the north or south pole of the earth lie in...?)

In your figure, fixing $r = 1$, you have $$ (x, y, z) = \sigma(\theta, \varphi) = (\cos\theta \sin\varphi, \sin\theta \sin\varphi, \cos\varphi). $$ (I've used "$\sigma$" for "spherical" rather than "$\phi$", in case my fingers mis-type "$\varphi$".)

The "non-covering" happens because if $k$ is an integer, then $\sigma(\theta, k\pi) = \bigl(0, 0, (-1)^{k}\bigr)$ for all real $\theta$. (As a consistency check, it's easy to verify the differential $D\sigma$ has rank one along the lines $\varphi = k\pi$.)

What's true is: For every integer $k$, the restriction $\sigma:\mathbf{R} \times \bigl(k\pi, (k+1)\pi\bigr) \to S^{2} \setminus \{(0, 0, \pm1)\}$ is a universal covering map for the sphere minus the north and south poles, a surface diffeomorphic to a cylinder. Each open rectangle of "width" $2\pi$ (and "height" $\pi$) in this strip is mapped diffeomorphically onto the sphere minus a closed half of a great circle joining the north and south poles.

(I haven't digested your edit carefully enough to know for certain what you mean by $T^{2}/\mathbf{Z}^{2}$, but in the usual reckoning, the integer lattice descends to a single point of the torus.)

Edit: In case a picture helps, the torus below is mapped, via its Gauss map, to the unit sphere. The "north" and "south" latitudes (in blue) are squeezed to points. Their complement wraps around the sphere twice; the shaded "inner" portion maps with degree $-1$, the unshaded "outer" portion maps with degree $+1$.

A torus mapping to a sphere

If $1 < R$, the torus can be parametrized by \begin{align*} \tau(\theta, \varphi) &= \bigl((R + \sin\varphi) \cos\theta, (R + \sin\varphi) \sin\theta, \cos\varphi) \\ &= (R\cos\theta, R\sin\theta, 0) + (\cos\theta \sin\varphi, \sin\theta \sin\varphi, \cos\varphi) \\ &= (R\cos\theta, R\sin\theta, 0) + \sigma(\theta, \varphi). \end{align*} The torus is a realization of $\mathbf{R}^{2}/(2\pi\mathbf{Z})^{2}$, and the parametrization $\tau$ is a universal covering map.

The summand $\sigma(\theta, \varphi)$, which coincides with spherical coordinates, is the value of the "outward-pointing" Gauss map at $\tau(\theta, \varphi)$. The Gauss map itself "discards" the term $(R\cos\theta, R\sin\theta, 0)$, and may be viewed as radially translating the longitudinal sections of the torus so they have a common axis (as if throttling a Slinky), so each blue point maps to a pole of the unit sphere.

Perhaps this makes clearer why the spherical coordinates map fails to be a covering map on any open set containing a point $\varphi = k\pi$ for some integer $k$.

Andrew D. Hwang
  • 82,053
  • Thanks for your answer. Let me describe the action (I don't know if this is really an action, by the way) by $\mathbb{Z}^2$. To simplify I will consider a special case. The arrow from $(0, 0)$ to $(0, \frac{\pi}{2})$ goes (under the action) to the arrow from $(\pi, 2\pi)$ to $(\pi, \frac{3\pi}{2})$, then applying this "action" again, it goes to the arrow from $(0, 2\pi)$ to $(0, 2\pi + \frac{\pi}{2})$. So in $\mathbb{T}^2$ it's an involution. Sorry for the messy description, I would post an image if I could draw in LaTeX or if I had a scanner. – user40276 Jun 02 '15 at 02:08
  • In case it helps: The rectangle $U_{a, b}$ is not mapped injectively by spherical coordinates unless $b$ is an integer multiple of $\pi$. If $b$ is not an integer multiple of $\pi$, there is a unique integer $k$ with $b < k < b+1$, and the open segment $(a, a + 2\pi) \times{k\pi} \subset U_{a,b}$ is mapped to the point $(0, 0, (-1)^{k})$. As a map on the torus $\mathbf{R}^{2}/(2\pi\mathbf{Z})^{2}$, spherical coordinates collapses two latitudes, giving a bouquet of two $2$-spheres; I believe your involution exchanges these spheres, so overall the quotient is $S^{2}$. – Andrew D. Hwang Jun 02 '15 at 09:45
  • Sorry, but I don't understand your argument. If $0 <b < \pi$, for instance, $\phi$ maps injectively onto the sphere minus a line segment given by $\phi (0 \times [b, \pi + b])$. – user40276 Jun 02 '15 at 10:03
  • Whoops...meant to type: "If $b$ is not an integer multiple of $\pi$, there is a unique integer $k$ with $b < k\pi < b + \pi$." So, if $0 < b < \pi$, then regardless of $a$, the rectangle $U_{a,b} = (a, a + 2\pi) \times (b, b + \pi)$ contains a segment $(a, a + 2\pi) \times {\pi}$ that maps to the south pole $(0, 0, -1)$ under spherical coordinates. Particularly, the spherical coordinates map is not injective on this rectangle. – Andrew D. Hwang Jun 02 '15 at 11:03
  • This is weird. So any open set covering a multiple of $\pi$ (in the second coordinate) will never be a bijection onto it's image, so it's impossible to make an atlas with spherical coordinates. I always thought that spherical coordinates would give an atlas to the sphere when restricting to some open sets. – user40276 Jun 02 '15 at 11:47
  • Exactly. :) The unit circle is the only sphere topologically covered by a Euclidean space. Related/consequent phenomena include simple-connectedness of $S^{n}$ for $n > 1$ (as you noted); curvature (the round circle is intrinsically flat, round $S^{n}$ is not flat if $n > 1$); the hairy ball theorem (if $\sigma$ were a covering map, there'd be non-vanishing continuous vector fields on $S^{2}$); and so on. – Andrew D. Hwang Jun 02 '15 at 13:54
  • I have edited the question. I made a mistake. The action should be given for all points by identifying $(\theta, \varphi)$ with $(\theta + \pi, 2\pi - \varphi)$. Hope the question is clear now. – user40276 Jun 06 '15 at 03:47
  • The issue is, the open rectangles $(a, a + 2\pi) \times (k\pi, (k+1)\pi)$ map diffeomorphically into the sphere (covering the complement of a closed arc from pole to pole), but the corresponding closed rectangles undergo boundary identification inconsistent with a covering map: The top and bottom edges map to points under $\sigma$. So, you've got a smooth mapping from the torus to the sphere, but in no way, shape, or form is the map a covering map (see my first comment above, re: a bouquet of spheres). – Andrew D. Hwang Jun 06 '15 at 12:39
1

There is nothing wrong with that notation (assuming the mathematical one, according to the Wikipedia link you included). Note that when $\theta=0$, increasing angle $\varphi$ goes from the Z axis to the X axis. In other words, the negative X axis corresponds to $\varphi=\frac{3\pi}{2}$ and, hence, $(-1,0,0)$ does belong to the circle.

AugSB
  • 5,107
  • But $\theta$ is not the angle between with the $x$-axis (in positive orientation), since $(-1, 0, 0)$ would have angle $\theta = \pi$ according to the picture. – user40276 Jun 01 '15 at 08:00
  • @user40276 You have both $(\pi,\dfrac{\pi}{2})$ and $(0,\dfrac{3\pi}{2})$ as coordinates that give $(-1,0,0)$ – Martigan Jun 01 '15 at 08:04
  • @Martigan So how are the sets such that $\phi$ is injective? They should induce a kind of tessellation of the plane and this is my main problem – user40276 Jun 01 '15 at 08:10
0

Honestly this is difficult to comment with no picture in the text, even if you linked one.

The problem is that you linked two of them...

And perhaps this is one of the answer you might have.

In physics and mathematics the conventions are not the same.

Don't try to set a value to $\theta$ and see wether it fits your understanding of the cartesian coordinates corresponding to it.

Try to take any point on the sphere and see if you can have $(\theta,\varphi)$ that works for it. You will see that it does, whatever your convention, and that, in turn, $\phi$ is a covering space as you call it.

Martigan
  • 5,969
  • I think he mentioned the "second picture". Also, have edited the post and included the picture. – Vlad Jun 01 '15 at 07:30
  • Maybe you misunderstood me. The problem is that $\theta$ is not the angle with the $x$-axis (oriented in the positive direction) as pictured in the figure in my question. Otherwise $\theta = 0$ would imply that $\phi (0 \times [0, 2\pi])$ is not the circle in $y = 0$ – user40276 Jun 01 '15 at 07:57
  • I get that. You have an answer that fits your question perfectly. $\theta=0$ is not the only way to be on the axis $x$. $\varphi=\pi/2$ is another one – Martigan Jun 01 '15 at 08:01
  • Yes, but what I'm worried about is not this. I just can't make sense of why $\theta$ is the angle with the $x$-axis if $(-1, 0, 0)$ have angle $\theta = 0$ with the $x$-axis. In other words, drawing the point $(-1, 0, 0)$ in the picture, it would have $\theta = \pi$. – user40276 Jun 01 '15 at 08:04
  • @user40276 Another way to see this is to understand that a negative $x$ does not mean that the angle $\theta=0$. $\theta=0$ means that your "starting point" is for $x=1$, but you can get negative value of $x$ when $\varphi$ changes... When $\theta=\pi$, you "start" with negative $x$.... – Martigan Jun 01 '15 at 08:09
  • I've just realized that $\phi$ cannot be a covering (as you claim), so I've edited my question . – user40276 Jun 02 '15 at 00:50