3

In the figure below, three vectors are joined together to form a triangle. The name of each vector is a single letter in boldface, each vector is specified by three lengths in an $xyz$ coordinate system, and vectors $\boldsymbol{a}$ and $\boldsymbol{b}$ are separated by angle $\theta$.

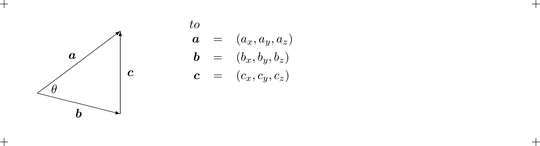
enter image description here

Let $a$, $b$, and $c$ (with neither boldface nor subscripts) represent the magnitudes (lengths) of vectors $\boldsymbol{a}$, $\boldsymbol{b}$, and $\boldsymbol{c}$. Note that the Pythagorean theorem is used. \begin{eqnarray*} a &=& \sqrt{a_x^2 + a_y^2 + a_z^2} \\ b &=& \sqrt{b_x^2 + b_y^2 + b_z^2} \\ c &=& \sqrt{c_x^2 + c_y^2 + c_z^2} \end{eqnarray*}

The expression $\boldsymbol{a} \cdot \boldsymbol{b}$ signifies the $scalar\ product$ (a.k.a. the $dot\ product$) of vectors $\boldsymbol{a}$ and $\boldsymbol{b}$. There are two common formulas for computing $\boldsymbol{a} \cdot \boldsymbol{b}$. The first is the sum of the products of the $xyz$ components. The second is the product of the magnitudes and the cosine of angle $\theta$. \begin{eqnarray*} \boldsymbol{a} \cdot \boldsymbol{b} &=& a_x b_x + a_y b_y + a_z b_z \\ \boldsymbol{a} \cdot \boldsymbol{b} &=& a b \cos \theta \end{eqnarray*}

It's not obvious that these two formulas for the scalar product are equivalent. Therefore, demonstrate that they are --- demonstrate that \begin{eqnarray*} a_x b_x + a_y b_y + a_z b_z &=& a b \cos \theta \end{eqnarray*}

Peter Franušić
  • 81

1 Answers1

1

Vector $\boldsymbol{a}$ is the sum of vectors $\boldsymbol{b}$ and $\boldsymbol{c}$. I.e., $\boldsymbol{a} = \boldsymbol{b} + \boldsymbol{c}$. Solving for $\boldsymbol{c}$ we have \begin{eqnarray*} \boldsymbol{c} &=& \boldsymbol{a} - \boldsymbol{b} \\ &=& (a_x, a_y, a_z) - (b_x, b_y, b_z) \\ &=& \big( (a_x-b_x),(a_y-b_y),(a_z-b_z) \big) \\ &=& \big( c_x , c_y , c_z \big) \end{eqnarray*}

We calculate magnitude $c$ using the $xyz$ components of vectors $\boldsymbol{a}$ and $\boldsymbol{b}$. \begin{eqnarray*} c &=& \sqrt{c_x^2 + c_y^2 + c_z^2} \\ &=& \sqrt{(a_x-b_x)^2 + (a_y-b_y)^2 + (a_z-b_z)^2} \end{eqnarray*}

We start with the squared magnitude $c^2$, expand it, rearrange it, then reduce it with the squared magnitudes $a^2$ and $b^2$. \begin{eqnarray*} c^2 &=& (a_x-b_x)^2 + (a_y-b_y)^2 + (a_z-b_z)^2 \\ &=& (a_x^2-2a_xb_x+b_x^2) + (a_y^2-2a_yb_y+b_y^2) + (a_z^2-2a_zb_z+b_z^2) \\ &=& (a_x^2+a_y^2+a_z^2) + (b_x^2+b_y^2+b_z^2) - 2(a_xb_x+a_yb_y+a_zb_z) \\ &=& a^2 + b^2 - 2(a_xb_x+a_yb_y+a_zb_z) \end{eqnarray*}

The Law of Cosines asserts that $c^2 = a^2 + b^2 - 2ab\cos\theta$. We replace $c^2$ with the result from above, subtract $a^2 + b^2$ from both sides, divide both sides by $-2$, and we're done. \begin{eqnarray*} \mathrm{Law\ of\ Cosines:\phantom{X}} c^2 &=& a^2 + b^2 - 2ab\cos\theta \\ a^2 + b^2 - 2(a_xb_x+a_yb_y+a_zb_z) &=& a^2 + b^2 - 2ab\cos\theta \\ -2(a_xb_x+a_yb_y+a_zb_z) &=& -2ab\cos\theta \\ a_xb_x + a_yb_y + a_zb_z &=& ab\cos\theta \end{eqnarray*}

QED

Peter Franušić
  • 81