Constructing the reciprocal of a segment

Question

How can one construct the reciprocal length of a line segment? For example, given any line segment a, how can $\frac{1}{a}$ be constructed?

I was told that it can be solved by creating similar triangles, but I do not get it.

Answer 1

There are several answers to your question. However, the question is meaningless unless the length $1$ is also given, since $\frac 1a$ has different units than $a$ does.

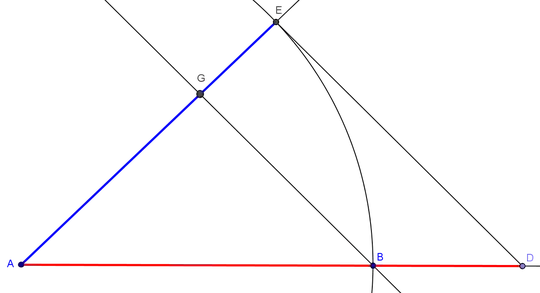
In this diagram, $AD$ is your given length $a$, and $AE$ is the unit length, $1$. Ray $\overrightarrow{AE}$ is an arbitrary ray that starts at point $A$. By construction, $AB=AE=1$ and segment $\overline{BG}$ is parallel to segment $\overline{DE}$.

Then triangles $ABG$ and $ADE$ are similar, so we have the proportion

$$\frac{AG}{AE}=\frac{AB}{AD}$$

or

$$\frac{AG}{1}=\frac{1}{a}$$

So $AG$ is your desired reciprocal $\frac 1a$.

Answer 2

Here is a simpler construction based on constructing perpendicular lines:

Suppose you have $x$, and you want $\frac 1x$. The circle has radius $1$. The hypotenuse of each of the triangles, together, define two perpendicular lines. The height the upper orange triangle is $x$, and the width of its base is $1$. The two orange triangles are identical, and the yellow and orange triangles are proportionally similar. The nice idea is that the product of the slopes of perpendicular lines has to be $-1$, so the height of the yellow triangle has to be $\frac1x$.

There are even simpler constructions, also based on similar triangles, for instance:

but it is a bit misleading because it looks different depending on whether $x<1$ or $x>1$. The perpendicular lines give a nice symmetry to the picture and the description.

Answer 3

Such a construction is possible by inversion of a point about a unit radius mirroring circle inside to outside and vice-versa.

A vertical line $PT$ should be drawn parallel to y-axis to cut unit circle at T. A tangent at T perpendicular to radius $OT$ cuts x-axis at Q, the mirror point shown as reciprocal of $OP$. If radius has a dimension as length the geometric property used here is $ OT^2= OP\cdot OQ$. Similarly $Q$ mirrors $P$.