Let $f: [1, \infty) \to \mathbb{R}$ be a continuous function such that the improper integral $$\int_1^\infty f(x) \ dx$$ exists. Show or disprove that $\lim \limits _{x \to \infty} f(x) =0$.
Our professor said that there are counterexamples but after frying my brain out I still could not find any. It does sound logical.
It does sound plausible, especially by analogy with infinite series. But yes, there are counterexamples. Here's one:
Consider a continuous function that is zero, except for triangles centered on the integers, of height 1 and area going like $1/2^n$. Then the integral will exist but the function itself doesn't converge to zero.
Added: A rough diagram (graph of function with is zero for all $x \geq 1$ except for two sides of isosceles triangles of height 1, base length $2^{-(n-2)}$ centered over each integer $n \geq 2$; the area of the triangle over the integer $n$ is $2^{-(n-1)}$.)
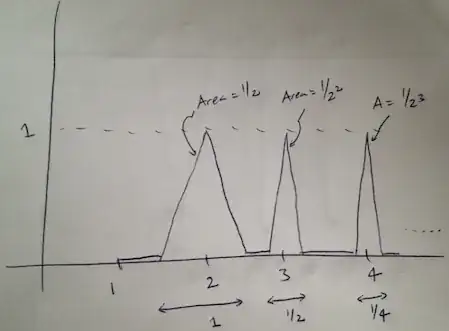
Then for such a function, $$\lim_{x\to\infty} \int_1^x f(x) \ dx = \lim_{N\to\infty} \sum_{n=2}^N 2^{-(n-1)} = 1$$
however $\lim_{x\to\infty} f(x)$ does not exist.
The counterexample can be made more exotic by allowing it be unbounded: let the isosceles triangle over integer $n$ have height $n/2$ and base length $(n2^{n-3})^{-1}$; each triangle's area remains $2^{-(n-1)}$.
Here is a simple counter example. $$f(x) = \begin{cases} 1 & \text{ if }x \in \mathbb{Z}^+\\ 0 & \text{ otherwise}\end{cases}$$
In case you are after an infinitely differentiable function, consider $f(x) = \sin(x^2)$. We have $$\int_0^{\infty} \sin\left(x^2 \right) dx = \dfrac12 \sqrt{\dfrac{\pi}2}$$ but $\lim_{x \to \infty} \sin\left(x^2 \right)$ doesn't exist.
You may even have positive continuous unbounded functions with an existing improper integral.
You can have a look here with some pictures.
