Area enclosed by an equipotential curve for an electric dipole on the plane

Question

I am currently teaching Physics in an Italian junior high school. Today, while talking about the electric dipole generated by two equal charges in the plane, I was wondering about the following problem:

Assume that two equal charges are placed in $(-1,0)$ and $(1,0)$.

There is an equipotential curve through the origin, whose equation is given by: $$\frac{1}{\sqrt{(x-1)^2+y^2}}+\frac{1}{\sqrt{(x+1)^2+y^2}}=2 $$ and whose shape is very lemniscate-like:

Is there a fast&tricky way to compute the area enclosed by such a curve?

Numerically, it is $\approx 3.09404630427286$.

Answer 1

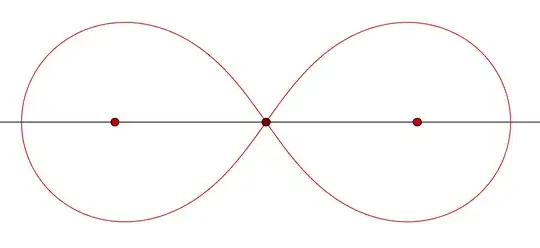
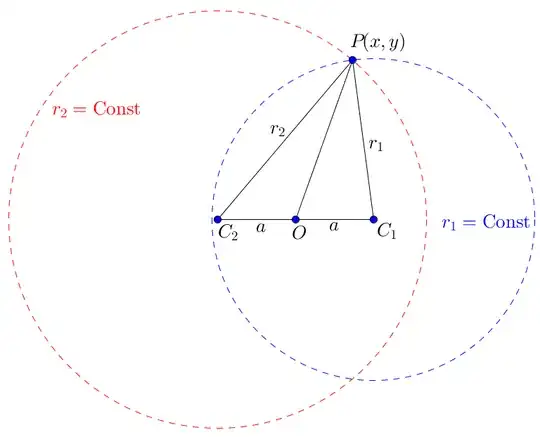
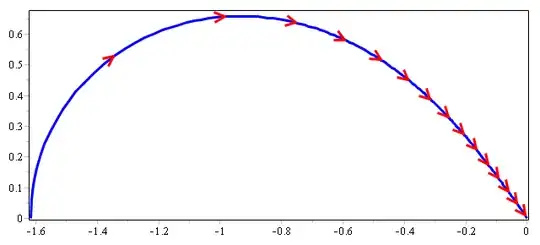
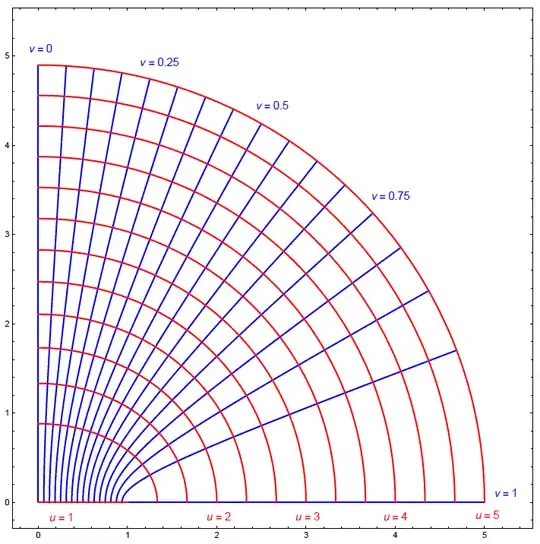
Consider this post an appendix to @achillehui's brilliant solution, which arrives at the following elliptic integral for the overall area:

$$\mathcal{A}=\sqrt{8}+\int_{1}^{\phi}\sqrt{\frac{1+x-x^{2}}{x\left(1+x\right)}}\,\mathrm{d}x=:\sqrt{8}+\mathcal{B},\tag{1}$$

where as usual $\phi$ denotes the golden ratio. I found this problem extremely interesting and just couldn't resist leaving that last integral unevaluated. The work below addresses the nuts and bolts of evaluating this elliptic integral as a particular case of a more general integral.

---

For real parameters $a,b,c,d,z\in\mathbb{R}\land d<c<b\le z<a$, define $\mathcal{E}{\left(a,b,c,d;z\right)}$ via the integral

$$\mathcal{E}{\left(a,b,c,d;z\right)}:=\int_{z}^{a}\sqrt{\frac{\left(a-x\right)\left(x-c\right)}{\left(x-b\right)\left(x-d\right)}}\,\mathrm{d}x.\tag{2}$$

For convenience we define ahead of time the auxiliary parameters

$$\begin{cases} &\theta:=\arcsin{\left(\sqrt{\frac{\left(a-c\right)\left(z-b\right)}{\left(a-b\right)\left(z-c\right)}}\right)},\\ &\kappa:=\sqrt{\frac{\left(a-b\right)\left(c-d\right)}{\left(a-c\right)\left(b-d\right)}},\\ &\nu:=\frac{a-b}{a-c}.\tag{3}\\ \end{cases}$$

The key to putting the elliptic integral $\mathcal{E}$ into something more closely resembling standard form the "magic" quadratic transformation,

$$\sqrt{\frac{\left(a-c\right)\left(x-b\right)}{\left(a-b\right)\left(x-c\right)}}=y\implies x=\frac{b\left(a-c\right)-c\left(a-b\right)y^{2}}{\left(a-c\right)-\left(a-b\right)y^{2}}.\tag{4}$$

$$\begin{align} \mathcal{E}{\left(a,b,c,d;z\right)} &=\int_{z}^{a}\sqrt{\frac{\left(a-x\right)\left(x-c\right)}{\left(x-b\right)\left(x-d\right)}}\,\mathrm{d}x\\ &=\int_{\sin{\theta}}^{1}\frac{2\left(a-b\right)\left(b-c\right)y}{\left(a-c\right)\left(1-\nu y^{2}\right)^{2}}\sqrt{\frac{\left(a-c\right)\left(1-y^{2}\right)}{\left(b-d\right)y^{2}\left(1-\kappa^{2}y^{2}\right)}}\,\mathrm{d}y\\ &=\frac{2\left(a-b\right)\left(b-c\right)}{\sqrt{\left(a-c\right)\left(b-d\right)}}\int_{\sin{\theta}}^{1}\frac{\mathrm{d}y}{\left(1-\nu y^{2}\right)^{2}}\sqrt{\frac{1-y^{2}}{1-\kappa^{2}y^{2}}}.\tag{5}\\ \end{align}$$

Defining another auxiliary function,

$$f{\left(\kappa,\nu;\theta\right)}:=\int_{\sin{\theta}}^{1}\frac{\mathrm{d}y}{\left(1-\nu y^{2}\right)^{2}}\sqrt{\frac{1-y^{2}}{1-\kappa^{2}y^{2}}},\tag{6}$$

we then find,

$$\begin{align} f{\left(\kappa,\nu;\theta\right)} &=\int_{\sin{\theta}}^{1}\frac{\mathrm{d}y}{\left(1-\nu y^{2}\right)^{2}}\sqrt{\frac{1-y^{2}}{1-\kappa^{2}y^{2}}}\\ &=\int_{\sin{\theta}}^{1}\frac{1-y^{2}}{\left(1-\nu y^{2}\right)^{2}}\cdot\frac{\mathrm{d}y}{\sqrt{\left(1-y^{2}\right)\left(1-\kappa^{2}y^{2}\right)}}\\ &=\int_{\sin{\theta}}^{1}\frac{\left(1-\nu y^{2}\right)+\left(\nu y^{2}-y^{2}\right)}{\left(1-\nu y^{2}\right)^{2}}\cdot\frac{\mathrm{d}y}{\sqrt{\left(1-y^{2}\right)\left(1-\kappa^{2}y^{2}\right)}}\\ &=\int_{\sin{\theta}}^{1}\frac{\mathrm{d}y}{\left(1-\nu y^{2}\right)\sqrt{\left(1-y^{2}\right)\left(1-\kappa^{2}y^{2}\right)}}\\ &~~~~~-\left(1-\nu\right)\int_{\sin{\theta}}^{1}\frac{y^{2}}{\left(1-\nu y^{2}\right)^{2}}\cdot\frac{\mathrm{d}y}{\sqrt{\left(1-y^{2}\right)\left(1-\kappa^{2}y^{2}\right)}}\\ &=\int_{\sin{\theta}}^{1}\frac{\mathrm{d}y}{\left(1-\nu y^{2}\right)\sqrt{\left(1-y^{2}\right)\left(1-\kappa^{2}y^{2}\right)}}\\ &~~~~~-\left(1-\nu\right)\frac{\partial}{\partial\nu}\int_{\sin{\theta}}^{1}\frac{\mathrm{d}y}{\left(1-\nu y^{2}\right)\sqrt{\left(1-y^{2}\right)\left(1-\kappa^{2}y^{2}\right)}}\\ &=\left[1-\left(1-\nu\right)\frac{\partial}{\partial\nu}\right]\int_{\sin{\theta}}^{1}\frac{\mathrm{d}y}{\left(1-\nu y^{2}\right)\sqrt{\left(1-y^{2}\right)\left(1-\kappa^{2}y^{2}\right)}}\\ &=\left[1-\left(1-\nu\right)\partial_{\nu}\right]\left[\Pi{\left(\nu,\kappa\right)}-\Pi{\left(\theta,\nu,\kappa\right)}\right].\tag{7}\\ \end{align}$$

Caution: out of force of habit, I use the argument conventions for denoting elliptic integrals that are adopted in Gradshteyn et. al, which differs slightly from that of many other common sources (such as an Wolfram-related reference or software).

Using the partial derivative formula

$$\small{\partial_{\nu}\Pi{\left(\theta,\nu,\kappa\right)}=\frac{E{\left(\theta,\kappa\right)}+\frac{\kappa^{2}-\nu}{\nu}F{\left(\theta,\kappa\right)}+\frac{\nu^{2}-\kappa^{2}}{\nu}\Pi{\left(\theta,\nu,\kappa\right)}-\frac{\nu\sin{\left(2\theta\right)}\sqrt{1-\kappa^{2}\sin^{2}{\left(\theta\right)}}}{2\left(1-\nu\sin^{2}{\left(\theta\right)}\right)}}{2\left(\kappa^{2}-\nu\right)\left(\nu-1\right)}},\tag{8}$$

we then find,

$$\begin{align} f{\left(\kappa,\nu;\theta\right)} &=\left[1-\left(1-\nu\right)\frac{\partial}{\partial\nu}\right]\left[\Pi{\left(\nu,\kappa\right)}-\Pi{\left(\theta,\nu,\kappa\right)}\right]\\ &=\frac{E{\left(\kappa\right)}+\frac{\kappa^{2}-\nu}{\nu}K{\left(\kappa\right)}+\frac{2\nu\kappa^{2}-\nu^{2}-\kappa^{2}}{\nu}\Pi{\left(\nu,\kappa\right)}}{2\left(\kappa^{2}-\nu\right)}\\ &~~~~~\small{-\frac{E{\left(\theta,\kappa\right)}+\frac{\kappa^{2}-\nu}{\nu}F{\left(\theta,\kappa\right)}+\frac{2\nu\kappa^{2}-\nu^{2}-\kappa^{2}}{\nu}\Pi{\left(\theta,\nu,\kappa\right)}-\frac{\nu\sin{\left(2\theta\right)}\sqrt{1-\kappa^{2}\sin^{2}{\left(\theta\right)}}}{2\left(1-\nu\sin^{2}{\left(\theta\right)}\right)}}{2\left(\kappa^{2}-\nu\right)}}.\\ \end{align}$$

---

Suppose now that $a+c+d=0\land c\ge b-a\land b\le0$. Then, setting $z=a+c$ we have

$$\begin{cases} &\theta=\arcsin{\left(\sqrt{\frac{\left(a-c\right)\left(a-b+c\right)}{\left(a-b\right)a}}\right)},\\ &\kappa=\sqrt{\frac{\left(a-b\right)\left(a+2c\right)}{\left(a-c\right)\left(a+b+c\right)}},\\ &\nu=\frac{a-b}{a-c}.\\ \end{cases}$$

Also setting $c=1-a\land b=0$, yields

$$\begin{cases} &\theta=\arcsin{\left(\frac{\sqrt{2a-1}}{a}\right)},\\ &\kappa=\sqrt{\frac{a\left(2-a\right)}{2a-1}},\\ &\nu=\frac{a}{2a-1}.\\ \end{cases}$$

Under these conditions, we can make the simplifications

$$\begin{align} f{\left(\kappa,\nu;\theta\right)} &=\frac{E{\left(\kappa\right)}+\frac{\kappa^{2}-\nu}{\nu}K{\left(\kappa\right)}+\frac{2\nu\kappa^{2}-\nu^{2}-\kappa^{2}}{\nu}\Pi{\left(\nu,\kappa\right)}}{2\left(\kappa^{2}-\nu\right)}\\ &~~~~~\small{-\frac{E{\left(\theta,\kappa\right)}+\frac{\kappa^{2}-\nu}{\nu}F{\left(\theta,\kappa\right)}+\frac{2\nu\kappa^{2}-\nu^{2}-\kappa^{2}}{\nu}\Pi{\left(\theta,\nu,\kappa\right)}-\frac{\nu\sin{\left(2\theta\right)}\sqrt{1-\kappa^{2}\sin^{2}{\left(\theta\right)}}}{2\left(1-\nu\sin^{2}{\left(\theta\right)}\right)}}{2\left(\kappa^{2}-\nu\right)}}\\ &=\frac{K{\left(\kappa\right)}-F{\left(\theta,\kappa\right)}}{2\nu}+\frac{\Pi{\left(\nu,\kappa\right)}-\Pi{\left(\theta,\nu,\kappa\right)}}{a}\\ &~~~~~+\frac{E{\left(\kappa\right)}-E{\left(\theta,\kappa\right)}}{2\left(\kappa^{2}-\nu\right)}+\frac{\sin{\left(2\theta\right)}\sqrt{1-\kappa^{2}\sin^{2}{\left(\theta\right)}}}{4\left(1-a\right)\left(1-\nu\sin^{2}{\left(\theta\right)}\right)}\\ &=\frac{\left(2a-1\right)\left[K{\left(\kappa\right)}-F{\left(\theta,\kappa\right)}\right]}{2a}+\frac{\Pi{\left(\nu,\kappa\right)}-\Pi{\left(\theta,\nu,\kappa\right)}}{a}\\ &~~~~~-\frac{\left(2a-1\right)\left[E{\left(\kappa\right)}-E{\left(\theta,\kappa\right)}\right]}{2a\left(a-1\right)}-\frac{1}{a}\sqrt{\frac{2a-1}{2a\left(a-1\right)}}.\\ \end{align}$$

Thus, for $1<a<2$ we obtain

$$\begin{align} \mathcal{E}{\left(a,0,1-a,-1;1\right)} &=\frac{2a\left(a-1\right)}{\sqrt{2a-1}}\,f{\left(\kappa,\nu;\theta\right)}\\ &=\left(a-1\right)\sqrt{2a-1}\left[K{\left(\kappa\right)}-F{\left(\theta,\kappa\right)}\right]\\ &~~~~~-\sqrt{2a-1}\left[E{\left(\kappa\right)}-E{\left(\theta,\kappa\right)}\right]\\ &~~~~~+\frac{2\left(a-1\right)\left[\Pi{\left(\nu,\kappa\right)}-\Pi{\left(\theta,\nu,\kappa\right)}\right]}{\sqrt{2a-1}}\\ &~~~~~-\sqrt{\frac{2\left(a-1\right)}{a}}.\tag{9}\\ \end{align}$$

---

Now, the particular case we're interested in is when $a$ takes the value of the golden ratio, $\phi=\frac{1+\sqrt{5}}{2}$, defined of course by the classical condition,

$$\phi=\frac{1}{\phi-1};~~~\small{\phi>0}.$$

A constant associated with $\phi$ is the so-called golden ratio conjugate,

$$\Phi:=\frac{1}{\phi}.$$

We finally obtain a closed form for the quantity $\mathcal{B}$ as follows:

$$\begin{align} \mathcal{B} &=\mathcal{E}{\left(\phi,0,1-\phi,-1;1\right)}\\ &=\mathcal{E}{\left(\phi,0,-\Phi,-1;1\right)}\\ &=\left(\phi-1\right)\sqrt{2\phi-1}\left[K{\left(\kappa\right)}-F{\left(\theta,\kappa\right)}\right]\\ &~~~~~-\sqrt{2\phi-1}\left[E{\left(\kappa\right)}-E{\left(\theta,\kappa\right)}\right]\\ &~~~~~+\frac{2\left(\phi-1\right)\left[\Pi{\left(\nu,\kappa\right)}-\Pi{\left(\theta,\nu,\kappa\right)}\right]}{\sqrt{2\phi-1}}\\ &~~~~~-\sqrt{\frac{2\left(\phi-1\right)}{\phi}}\\ &=\Phi\sqrt[4]{5}\left[K{\left(\kappa\right)}-F{\left(\theta,\kappa\right)}\right]-\sqrt[4]{5}\left[E{\left(\kappa\right)}-E{\left(\theta,\kappa\right)}\right]\\ &~~~~~+\frac{2\Phi}{\sqrt[4]{5}}\left[\Pi{\left(\nu,\kappa\right)}-\Pi{\left(\theta,\nu,\kappa\right)}\right]-\Phi\sqrt{2},\tag{10a}\\ \end{align}$$

where

$$\begin{cases} &\theta=\arcsin{\left(\frac{\sqrt{2\phi-1}}{\phi}\right)},\\ &\kappa=\sqrt{\frac{\phi\left(2-\phi\right)}{2\phi-1}},\\ &\nu=\frac{\phi}{2\phi-1}.\tag{10b}\\ \end{cases}$$

Result $(10)$ above is potentially a place to step, but the six separate elliptic integral terms make the expression too cumbersome to fool with if we don't have too. Since each elliptic integral term has the same elliptic modulus $\kappa$, simplification seems very likely. I'll update my response if I make any progress towards a simplified final value.

Answer 2

Consider following parametrization of the first quadrant of the $(x,y)$ plane:

$$[1,\infty) \times [0,1] \ni (u,v) \quad\mapsto\quad (x,y) \in [0,\infty)^2 \quad\text{s.t.}\quad \begin{cases} r_1 &= \sqrt{(x+1)^2+y^2} = u+v\\ r_2 &= \sqrt{(x-1)^2+y^2} = u-v \end{cases}$$ In this parametrization, the area element is given by $$dx \wedge dy = -\omega\quad\text{ where }\quad \omega \stackrel{def}{=} \frac{u^2-v^2}{\sqrt{(u^2-1)(1-v^2)}} du \wedge dv$$ Let $D$ be the region in $(u,v)$ plane corresponds to the dipole in first quadrant. Its boundary $\partial D$ consists of 3 pieces

1. $C_1$ : a curve start at $(1,0)$, end at $(\phi,1)$ where $\phi = \frac{1+\sqrt{5}}{2}$ is the Golden ratio. $$[1,\phi] \in t \quad\mapsto\quad (u,v) = \left(t,\sqrt{t(t-1)}\right) \in [1,\infty) \times [0,1]$$
2. $C_2$ : a line segment from $(\phi,1)$ to $(1,1)$.
3. $C_3$ : a line segment from $(1,1)$ to $(1,0)$.

Notice $\omega = \frac12 d\Omega$ where $$\Omega \stackrel{def}{=} \frac{u (u^2 - 1) dv - v(1-v^2) du}{\sqrt{(u^2-1)(1-v^2)}}$$ The area $\mathcal{A}$ we seek equals to $$\mathcal{A} = 4 \int_D \omega = 2\int_{\partial D}\Omega = 2\left(\int_{C_1} + \int_{C_2} + \int_{C_3}\right) \Omega$$

Introduce another parametrization for the region $[1,\infty) \times [0,1]$ in the $(u,v)$ plane:

$$[0,\infty) \times [0,\pi] \ni (\rho,\eta) \quad\mapsto\quad (u,v) = (\cosh\rho,\cos\eta) \in [1,\infty) \times [0,1]$$

One can use this to verify the line segments $C_2$ and $C_3$ contribute nothing to $\mathcal{A}$. As a result,

$$\mathcal{A} = 2\int_{C_1} \Omega = 2\int_{C_1} \left(u\sqrt{\frac{u^2-1}{1-v^2}} dv - v\sqrt{\frac{1-v^2}{u^2-1}} du\right)$$

Since $v^2 = u(u-1)$ on curve $C_1$, we can transform the $1^{st}$ piece of the integrand as $$\begin{align} u\sqrt{\frac{u^2-1}{1-v^2}} dv &= \sqrt{\frac{u(u+1)}{1-v^2}} vdv = \sqrt{u(u+1)} d(-\sqrt{1-v^2})\\ &= -d \sqrt{u(u+1)(1-v^2)} + \sqrt{1-v^2}d\sqrt{u(u+1)}\\ &= -d\sqrt{u(u+1)(1-v^2)} + \sqrt{\color{red}{\frac{1-v^2}{u(u+1)}}}\left(\color{red}{u} + \frac12\right) du \end{align} $$ Notice the piece in red can be rewritten as $\displaystyle\;\sqrt{\frac{u(1-v^2)}{u+1}} du = v\sqrt{\frac{1-v^2}{u^2-1}} du\;$ which is nothing but the $2^{nd}$ piece. This leads to

$$\begin{align} \mathcal{A} &= -2 \left[\sqrt{u(u+1)(1-v^2)}\right]_{(u,v) = (1,0)}^{(\phi,1)} + \int_{C_1} \sqrt{\frac{1-v^2}{u(u+1)}} du\\ &= \sqrt{8} + \int_1^\phi \sqrt{\frac{1+u-u^2}{u(u+1)}} du \tag{*1} \end{align} $$

As a double check, one can throw following command to wolfram alpha,

Sqrt[8]+Integrate[Sqrt[(1+u-u^2)/(u*(u+1))],{u,1,GoldenRatio}]

to evaluate in $(*1)$ numerically. WA returns $$\mathcal{A} \approx 3.0940463058814386237217800770286020796565427678...$$ a number matching what has been stated on question.

This is as far as I can get. I hope someone can further simplify the integral in $(*1)$. Please note that WA do know how to compute the anti-derivative for the integral at $(*1)$. It is a page long expression in terms of elliptic integrals and I won't reproduce it here.

Answer 3

At the first step, I will introduce a proper curve linear coordinates for this problem. This will help to construct the integral for area. We can write the equation of these equi-potential curves as

$$\frac{1}{r_1}+\frac{1}{r_2}=C \tag{1}$$

where $C$ is some real constant and $r_1$ and $r_2$ are defined as

$$r_1=\sqrt{(x-a)^2+y^2} \\ r_2=\sqrt{(x+a)^2+y^2} \tag{2}$$

where $2a$ is the distance between the two like charges on the $x$-axis placed at $x=a$ and $x=-a$. Equation $(2)$ is introducing a new curve-linear coordinates $(r_1,r_2)$ which is called the two-center bipolar coordinates. The geometric interpretation is easy as it just describes the coordinates of a point in $xy$ plane via the distance of that point through two other points which are called the centers. You can take look at this link in WIKI or this post on MSE. However, they doesn't contain that much information.

Then we find $x$ and $y$ from equations in $(2)$ in terms of $r_1$ and $r_2$. For this purpose, subtract and add the equations in $(4)$ to get

$$\begin{align} r_2^2-r_1^2&=4ax \\ r_2^2+r_1^2&=2(x^2+y^2+a^2) \end{align} \tag{3}$$

after some simplifications, $x$ and $y$ in terms of $r_1$ an $r_2$ will be

$$ \begin{align} x &= \frac{1}{4a} (r_{2}^{2}-r_{1}^{2})\\ y &= \pm \frac{1}{4a} \left( \sqrt{16 a^2 r_{2}^{2}-(r_{2}^{2}-r_{1}^{2}+4a^2)^2} \right) \end{align} \tag{4}$$

For a given $(r_1,r_2)$ we will find two pairs $(x,y)$ and $(x,-y)$. It is evident from the above picture that why this happens.

The next step will be the construction of the integral for area. We set $C=2a=2$ and find the intersection of the $\infty$ shaped curve with the $x$-axis

$$y=0 \qquad \to \qquad \frac{1}{\sqrt{(x-1)^2}}+\frac{1}{\sqrt{(x+1)^2}}=2 \qquad \to \qquad x=-\phi,0,\phi \tag{5}$$

where $\phi=\frac{1+\sqrt{5}}{2}$ is the golden ratio number. So according to $(1)$, $(4)$, and $(5)$ the parametric equations of the curve in the second quadrant of $xy$ plane will be

$$ \begin{align} x &= \frac{1}{4} \left(r_{2}^{2}-\left(\frac{r_2}{2r_2-1}\right)^{2}\right)\\ y &= \frac{1}{4} \sqrt{16 r_{2}^{2}-\left(r_{2}^{2}-\left(\frac{r_2}{2r_2-1}\right)^{2}+4\right)^2} \end{align} \qquad \qquad \phi-1 \le r_2 \le 1 \tag{6}$$

Finally, the integral to be evaluated for the area will be

$$\begin{align} \text{Area} &=4 \int_{-\phi}^{0} y dx \\ &=4 \int_{\phi-1}^{1}y \frac{dx}{dr_2}dr_2 \\ &= \int_{\phi-1}^{1} \sqrt{16 r_{2}^{2}-\left(r_{2}^{2}-\left(\frac{r_2}{2r_2-1}\right)^{2}+4\right)^2} \left(\frac{r_2}{2}-\frac{r_2}{2(2r_2-1)^2}+\frac{r_{2}^{2}}{(2r_2-1)^3}\right) dr_2 \end{align}$$

The numerical value of area up to fifty digits is

$$\text{Area}=3.0940463058814386237217800770286020796565427678113$$

as stated in the question. However, finding a tricky way to evaluate the definite integral of the area in a closed form should be investigated. I did the computations in this MAPLE file which may be useful for anyone who reads this post.

Answer 4

Here is another method based on the curve-linear coordinates introduced by Achille Hui. He introduced the following change of variables

$$\begin{align} \sqrt{(x+1)^2+y^2} &= u+v\\ \sqrt{(x-1)^2+y^2} &= u-v \end{align} \tag{1}$$

Then solving for $x$ and $y$ we shall get

$$\begin{align} x &= u v\\ y &= \pm \sqrt{-(u^2-1)(v^2-1)} \end{align} \tag{2}$$

required that

$$-(u^2-1)(v^2-1) \ge 0 \tag{3}$$

It does not look familiar but in fact it is! Taking into account the equations $(2)$ and $(3)$, we can consider the following as a parameterization for the first quadrant of the $xy$ plane

$$\boxed{ \begin{array}{} x=uv & & 1 \le u \lt \infty \\ y=\sqrt{-(u^2-1)(v^2-1)} & & 0 \le v \le 1 \end{array}} \tag{4}$$

I tried to draw the coordinate curves of this curve-linear coordinates and I just noticed that it is exactly the same as the Elliptic Coordinates and nothing else! You can show this analytically by the change of variables

$$\begin{align} u &= \cosh p \\ v &= \cos q \end{align} \tag{5}$$

I leave the further details in this avenue to the reader.

Let us go back to the problem of calculating the area. The equation of the $\infty$ curve was

$$\frac{1}{\sqrt{(x-1)^2+y^2}}+\frac{1}{\sqrt{(x+1)^2+y^2}}=2 \tag{6}$$

so combining $(1)$ and $(6)$ leads to

$$v=\pm \sqrt{u^2-u} \tag{7}$$

and hence the parametric equation of the $\infty$ curve in the first quadrant by considering $(4)$ and $(7)$ will be

$$\boxed{ \begin{array}{} x=u\sqrt{u^2-u} & & 1 \le u \lt \phi \\ y=\sqrt{-(u^2-1)(u^2-u-1)} \end{array}} \tag{8}$$

and finally the integral for the area is

$$\begin{align} \text{Area} &=4 \int_{0}^{\phi} y dx \\ &=4 \int_{1}^{\phi}y \frac{dx}{du}du \\ &=2 \int_{1}^{\phi} (4u-3)\sqrt{-u(u+1)(u^2-u-1)}du \\ &\approx 3.09405 \end{align} \tag{9}$$

Answer 5

HINT:

Almost sure area can be evaluated between limits $(u_1,u_2),(v_1,v_2)$ for holomorphic functions of complex variables in conformal maps.

The equipotentials and lines of force form an orthogonal net of curvilinear rectangle curves (resemble Cassinian Ovals, but different.. one out of which is shown above), and force lines which are all concurrent hyperbolas passing through the pole of same polarity / charge and asymptotic to y-axis. For these $(u,v)$ parameter plots that satisfy Laplace equation all we need before evaluating integral of area is to identify limits of u and v for any oval chosen. (shall upload equation , if it is found in sites e.g. 2d curves.com)

EDIT1:

The closest that I can get to the function is sketched by Mark McClure in another context for $ f(z)= z^2 (z-1)^3 $:

Orth Traj to Hyperbolae

I think we should choose another complex variable part so that our hyperbolae pass through $ (\pm 1,0)$ instead of $ ( 0,0),(1,0)$ as given above. We are interested in a particular orthogonal trajectory doubly intersecting at origin. Calculation of area may be easier.