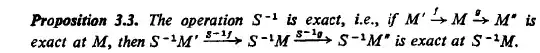6

I want to show this lemma:

Let $R$ be a domain. If $A$ is a torsion $R$-module, then $\operatorname{Tor}_1^R (K,A)\cong A$ where $\operatorname{Frac}(R)=Q$ and $K=Q/R$.

When I was reading this proof need to show $Q$ is flat and it back to this problem

if $R$ is a domain with $Q=\operatorname{Frac}(R)$, then $Q$ is flat $R$-module?

I don't know why $Q$ is flat. Can you help please?
thank you

rschwieb
  • 160,592
pink floyd
  • 1,314

2 Answers2

9

If you have a short exact sequence of modules and localize it, it remains exact.

What is the relation between localizing a module and tensoring it with the field of fractions?

Mariano Suárez-Álvarez
  • 139,300
  • why if $0\to M\to N\to L\to 0$is exact sequence then $0\to M\otimes Q\to N\otimes Q$is exact? – pink floyd Apr 30 '15 at 18:00
  • Have you read my answer? :-| – Mariano Suárez-Álvarez Apr 30 '15 at 18:04
  • I don't know localize! – pink floyd Apr 30 '15 at 18:08
  • Then ask for a clarification or an alternative explantion. Repeating your original question in a comment is somewhat confusing! – Mariano Suárez-Álvarez Apr 30 '15 at 18:09
  • @parisa this answer deserves acceptation. if you are not familiar with localization you can add in your question that you prefer the answers not using localization – user 1 Apr 30 '15 at 18:09
  • 5
    In any case, I suggest you read up on localization, parisa. It is slightly weird to know about flatness and Tor and not about localizations! – Mariano Suárez-Álvarez Apr 30 '15 at 18:10
  • @MarianoSuárez-Álvarez Old discussion but just wanted to comment that my graduate programs teaches the 'traditional' ring/module theory (focusing on all things noncommutative) in one course but reserves teaching about localizations until your introductory course in commutative algebra. So many of my fellow students (at one point myself included) knew much about flatness, ext, tor, and the like but nothing of localization other than vague comments that it was 'like' FOF and that we would see it later. – mathematics2x2life Dec 21 '16 at 06:35
6

Mariano Suárez-Alvarez's answer is correct. I only add that in general $S^{-1}$ is exact:
Atiyah-Macdonald has:

enter image description here

and
enter image description here

The particular case is field of fraction of a domain

user 1
  • 7,652