Consider a grid $G$ in the $\mathbb{R}^2$ plane formed by the points $(x,y)$ with integer coordinates i.e. $G=\{(x,y)\in\mathbb{R}^2: x\in\mathbb{Z},\;y\in\mathbb{Z} \}$. For $n>0$ let $B_n$ square centered at $(0,0)$ whose sides have length $2^{n+1} + 1$. Note that $B_n=\{-2^n,\ldots,0,\ldots,+2^n \}\times \{-2^n,\ldots,0,\ldots,+2^n \}$.
Consider all the circuits as a finite set of points $p_{0},p_1,\ldots, p_{k-1},p_k,p_{k+1}\ldots, p_n$ such that:
- the starting point $p_0$ is equal to its endpoint $p_n$, that is, $p_0=p_n $;
- the circuit trace has no self-intersection;
- $p_k$ and $p_{k+1}$ are neighbors for $k=0,1,3,\ldots,n $. By neighboring points we understand the points that are distance 1 according to the metric $d(p,q)=\max\{|x_p-x_q|,|y_p-y_q| \}$ for points $p=(x_p,y_p)$ and $q=(x_q,y_q)$ in $\mathbb{Z}^2$.
For an illustration with rectangles $B_2$ and $B_3$ see the figure below.
.........................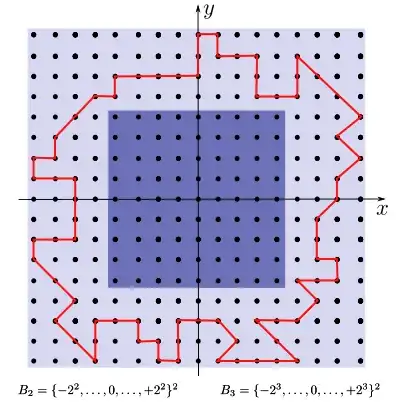
Question. What is the maximum number of circuits that can be drawn within the square $B_{n+1}$ and out of $B_n$ square?
My attempt was to divide the region where the circuit can pass in 8 rectangles. As shown below. And then try to count the number of paths running from side to side of each rectangle.
.........................!