Reflection of a curve around a slant line

Question

a fifth-degree function:

y = 80*x^5-225*x^4+350*x^3-300*x^2+150*x-20 (the green curve in the image)

needs to be reflected/mirrored around the line

y=55x-20 (the blue line)

and I am only interested in the segment [0,1]. While there is plenty of content on the internet on how to reflect around the axes or vertical/horizontal lines, I have not found an algebra explanation of how to do this around a slant line.

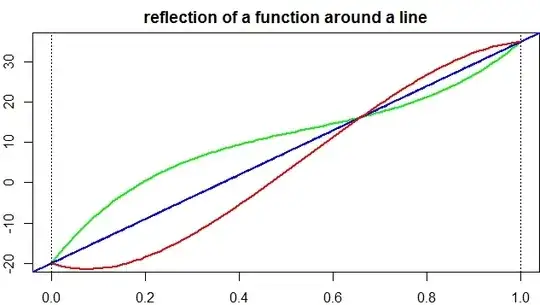
This image is an approximation: the red curve's shape should be slightly different: this is just the difference between the line and the curve, not the reflection.

How do I find the equation of the reflected green curve?

And part 2 of this question: Is it true that applying the equation of the reflection onto the original equation (the green curve) will return the equation of the slant blue line?

so if f*(x) is the reflection: is f*(f(x)) ?= ax+b

A step-by-step explanation would help anyone with a similar problem who sees this post. There's a similar post here, about reflecting around horizontal/vertical lines.

Thank you!

Answer 1

$\newcommand{\vec}[1]{\mathbf{#1}}$The reflected curve is not generally a graph, but it's easy to obtain a parametric description. For generality, let's say the graph $y = f(x)$ is to be reflected across the line $\ell$ with symmetric equation $ax + by + c = 0$ ($a$ and $b$ not both zero). Dividing the equation of $\ell$ by $\sqrt{a^{2} + b^{2}}$, we may assume $(a, b)$ is a unit vector.

Pick a point $(x_{0}, y_{0})$ on $\ell$, and make a translational change of coordinates so this point is the origin: $(u, v) = (x - x_{0}, y - y_{0})$. The graph becomes $v + y_{0} = f(u + x_{0})$, and the line is $au + bv = 0$.

The (unit) vector $\vec{p} = (-b, a)$ lies on $\ell$, and $\vec{n} = (a, b)$ is orthogonal to $\ell$. Each point $\vec{x} = (u, v)$ is uniquely represented as \begin{align*} \vec{x} &= (\vec{x} \cdot \vec{p}) \vec{p} + (\vec{x} \cdot \vec{n}) \vec{n} \\ &= (-bu + av)(-b, a) + (au + bv)(a, b). \end{align*} The image of $\vec{x}$ under reflection across $\ell$ is \begin{align*} R_{\ell}(\vec{x}) &= (\vec{x} \cdot \vec{p}) \vec{p} - (\vec{x} \cdot \vec{n}) \vec{n} \\ &= (-bu + av)(-b, a) - (au + bv)(a, b) \\ &= \bigl((b^{2} - a^{2})u - 2abv, -2abu - (b^{2} - a^{2})v\bigr). \tag{1} \end{align*} (If we write $(a, b) = (\cos\theta, \sin\theta)$, the coefficients in the preceding expression are $\pm\cos(2\theta)$ and $-\sin(2\theta)$.)

The graph is parametrized by $$ (u, v) = \bigl(t + x_{0}, f(t + x_{0}) - y_{0}\bigr); $$ substituting these functions into (1) gives a parametrization of the reflected graph.

Answer 2

In a previous answer in How do I reflect a function about a specific line? I showed how to derive a formula for $y=f(x)$, if its rotated by $y=mx+b$

Using the formula

$$\left(\frac{2m}{2m^2+1}x'-\frac{1-m^2}{m^2+1}(y'-b)+b\right)=f\left(\frac{2m}{m^2+1}(y'-b)-\frac{1-m^2}{m^2+1}x'\right)$$

If we substitute $f(x)=80x^5-225x^4+350x^3-300x^2+150x-20$, $m=55$ and $b=-20$ you will end up with the following graph. You should get the same picture you found above.

Answer 3

There is equivalent approach if you have a set $ { \left\{ \left( {x}_{i}, {y}_{i} \right) \right\} }_{i = 1}^{n} $.
Given a slant line with angle of $ \theta $ form the origin you can do the following steps:

1. Rotate the vectors by $ \theta $ clock wise using a Rotation Matrix.
2. Reflect the results over the $ y = 0 $ line by negating the $ y $ coordinate.
3. Rotate the data back using the inverse of the Rotation Matrix.

All that can be integrated into one matrix where the steps above are just its Eigen Decomposition. This is for finite set of points.
Actually for a function, it is the same if you write it a parameterized manner of a vector.

Funny thing happens if you chose the line to be $ g \left( x \right) = x $.
To reflect a function $ y = f \left( x \right) $ over $ g \left( x \right) $ let's right it as $ \left( y, f \left( x \right) \right) $.
Now the reflection is given by $ \left( f \left( x \right), y \right) $.

Why is that?

To rotate by 45 degrees a point given by $ \left(x, y \right) $ let's write it in the complex plane form - $ x + iy $.
To rotate a complex point by 45 Degrees clock one should multiply it by $ \frac{1 - i}{\sqrt{2}} $.
The coordinates of the new point are given by $ \frac{x + y}{\sqrt{2}} + i \frac{y - x}{\sqrt{2}} \rightarrow \left( \frac{x + y}{\sqrt{2}}, \frac{y - x}{\sqrt{2}} \right) $

Now, reflect it over the y axis by negating the second element which yields $ \left( \frac{x + y}{\sqrt{2}}, \frac{x - y}{\sqrt{2}} \right) $.

Now rotate back this by multiplying by $ 1 + i $ which yields $ y + ix $ namely the new coordinates are $ \left( y, x \right) $.

Enjoy...