4

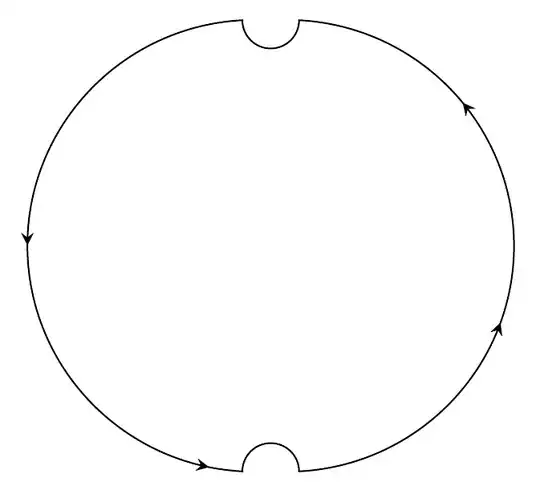
This is the integration I am trying to solve $$\int_{0}^{\pi} \sin^{2}(\theta)\sec^{3}(\theta)d\theta$$

putting $$z=e^{i\theta}$$ $$\int_{\gamma} \frac{-2{(z^{2}-1)}^2}{i(z-i)^{3}(z+i)^{3}}d\theta$$

when applying the residue theorem over a circle of radius 1, singularities are on the circle instead of inside the circle.How can we evaluate a integration like this

Thanks

dustin
  • 8,559
MaxQuantum
  • 77
  • 1
    Draw a little indentation around them of radius epsilon. Then by Cauchy, the the integrals that make up the contour equal zero. – dustin Feb 20 '15 at 01:29
  • @dustin Thanks. You mean drawing two identations on the main circle around i,-i?can you please elaborate the answer? – MaxQuantum Feb 20 '15 at 01:40
  • 1
    Yes excluding them. Then you can say original integral equals my contour integrals equals zero. I am working on your other question at the moment. – dustin Feb 20 '15 at 01:41

1 Answers1

5

Your integral can be written as $$ \int_0^{\pi}\sin^2(\theta)\sec^3(\theta)d\theta = \frac{1}{2}\int_0^{2\pi}\sin^2(\theta)\sec^3(\theta)d\theta = i\int_C\frac{(z^2-1)^2}{(z^2+1)^3}dz $$ Taking the following contour:

enter image description here

Then \begin{align} \int_0^{\pi}\sin^2(\theta)\sec^3(\theta)d\theta &= \frac{1}{2}\int_0^{2\pi}\sin^2(\theta)\sec^3(\theta)d\theta\\ & = i\int_C\frac{(z^2-1)^2}{(z^2+1)^3}dz\\ & = i\pi\sum\text{Res}\\ & = i\pi\biggl[\lim_{z\to i}\frac{d^2}{dz^2}(z-i)^3\frac{(z^2-1)^2}{(z^2+1)^3} + \lim_{z\to -i}\frac{d^2}{dz^2}(z+i)^3\frac{(z^2-1)^2}{(z^2+1)^3}\biggr] \end{align}

dustin
  • 8,559
  • 1
    @MaxQuantum with these poles, we have half a circle so instead of $2\pi i\sum\text{Res}$ it is $\pi i\sum\text{Res}$ whereas inside the contour it is the $2\pi i\sum\text{Res}$. If you look on the right, you will see linked post. Click the link. It is a similar question that may shed more light. It will be your name form your question post. – dustin Feb 20 '15 at 05:40
  • I think the above method has problems. We can t draw a circle, because at theta=pi/2 denominator of the function becomes zero.We may have to use Cauchy principle value – MaxQuantum Feb 20 '15 at 23:55
  • thanks. Could you please send an example like this. I always find when there is another constant with cos(\theta) term in the denominator. for example http://home.ku.edu.tr/~amostafazadeh/math303/math303_F2013/Handouts/Boas_Complex%20Integration.pdf page 13 (sec 7) tells we can draw the circle only if the denominator is non zero – MaxQuantum Feb 21 '15 at 00:29
  • 1
    @MaxQuantum consider this problem. If $z=\cos$ or $\sin$, then denominator would be zero for some $\theta$ but yet we can still draw a circular contour. – dustin Feb 21 '15 at 01:01
  • I get 0 answer when evaluating the integration using the method you suggested and when I try it in mathematica with principle value it gives a complex number. That is okay Ill check on it. Thanks – MaxQuantum Feb 21 '15 at 01:14
  • 1
    @MaxQuantum zero is correct. See here – dustin Feb 21 '15 at 01:16
  • @MaxQuantum it just means mathematica can't evaluate it but it may not converge. I don't know. Can you delete some comments? We aren't supposed to have long comment chains. – dustin Feb 21 '15 at 01:25
  • I added e^(icos(theta)) to the initial integration, and drew the full circle with deformations as you suggested gives 0. And Wolform alpha does not give an answer. This is my problem. I will look in to it. Thanks for your great help – MaxQuantum Feb 21 '15 at 01:30