Covering space of an orientable manifold

Question

I want to show that every covering space of an orientable manifold is an orientable manifold. My definition of orientability is throw homology. It's a new notion for me, I need help... Thank you.

Answer 1

I have just read the texts about orientation in Hatcher's Algebraic topology and tried to give a proof purely by the definition there.

Proof. $\;$ Let $\pi\colon N\to M$ be a covering of an orientable $n$-manifold $M$. Fix an orientation $x\mapsto \mu_x$ of $M$. For each $\widetilde{x}\in N$ a lift of $x$, there is a neighborhood $U$ of $x$ which is homeomorphic to an open ball in $\mathbb{R}^n$ which lifts to $\widetilde{U}$, and $\pi|_{\widetilde{U}}$ is a homeomorphism. We have isomorphisms $$H_n(\widetilde{U}|\widetilde{x})\overset{i_*}{\longrightarrow}H_n(N|\widetilde{x}),\ H_n(U|x)\overset{i_*}{\longrightarrow} H_n(M|x),$$ by excision. Then we define a map $\widetilde{x}\mapsto \mu_{\widetilde{x}}$ where $\mu_{\widetilde{x}}$ is the image of $\mu_x$ under the isomorphism $$H_n(M|x)\overset{(i_*)^{-1}}{\longrightarrow} H_n(U|x)\overset{(\pi_*)^{-1}}{\longrightarrow} H_n(\widetilde{U}|\widetilde{x})\overset{i_*}{\longrightarrow} H_n(N|\widetilde{x}).$$ To show the map is well defined, suppose $U,V$ are two such neighborhoods of $x$, WLOG, we may assume that $V\subset U$ and it suffices to show that we are assigning to $\widetilde{x}$ the same local orientation by the above construction using $U, V$ respectively. Consider the following diagram

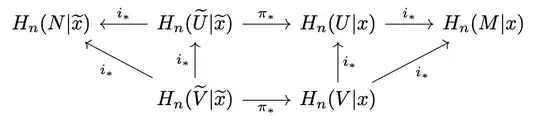
where the $i_*$'s are all induced by inclusion and are isomorphisms. Commutativity is clear and that will get it done.

To see the map satisfies the local consistency condition, consider the following diagram

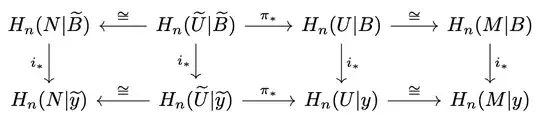
where $B\subset U$ is a neighborhood of $x$ such that $\overline{B}\subset U$ and for each $y\in B$ the local orientation $\mu_y$ is the image of one choosen generator $\mu_B$ under $H_n(M|B)\to H_n(M|y)$. The four outer horizonal isomorphisms come from excision and they are all induced by inclusions, the middle $\pi_*$'s are isomorphisms since $\pi$ restrict to homeomorphisms on the corresponding subsets, and commutativity of the diagram is clear. By the construction above, $\mu_y$ correspondes to $\mu_{\widetilde{y}}$ under the lower horizonal isomorphisms, then we conclude that $\mu_{\widetilde{y}}$ is the image of $\mu_{\widetilde{B}}$ under the natural map $i_*\colon H_n(N|\widetilde{B})\to H_n(N|\widetilde{y})$, where $\mu_{\widetilde{B}}$ is the generator corresponding to $\mu_B$ under the upper horizonal isomorphisms.

Answer 2

As I started typing to answer your question, I realized that I had already answered the same question some time ago. So here is a perfectly fine answer to your question using the homology definition: How to show the covering space of an orientable manifold is orientable

Regard this answer as a kind invite to search MSE for a second before asking a question.