Let $f:\mathbb{R}\to\mathbb{R}$ be the polynomial defined by $$f(x)=x^2-x-1$$ and let $$g_0(x)=f(x),\quad g_1(x)=f(f(x)),\quad\ldots\quad g_n(x)=f(f(f(\cdots f(x)\cdots)))$$ The positive root of $f(x)$ is the famous golden ratio $$\varphi=\frac{1+\sqrt{5}}{2}.$$
Problem: Find all $x\in\mathbb{R}$ for which the limit $$\lim_{n\to\infty}g_{3n}(x)$$ exists.
The answer appear to be not at all trivial. Based on numerical computations, I conjecture that the limit exists if and only if $$x\in[-\sqrt{2},1+\sqrt{2}]-\mathbb{N}.$$ But for some $x$, the convergence is very strange. For example, look at this plot of the sequence $\{g_{3n}(0.18)\}$ for $0\leq n\leq 200$:
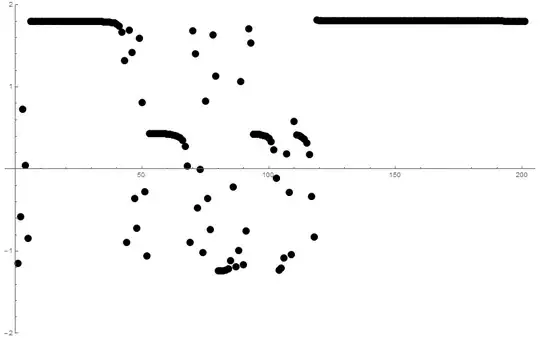
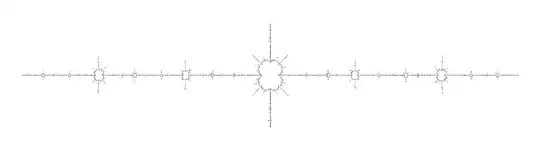
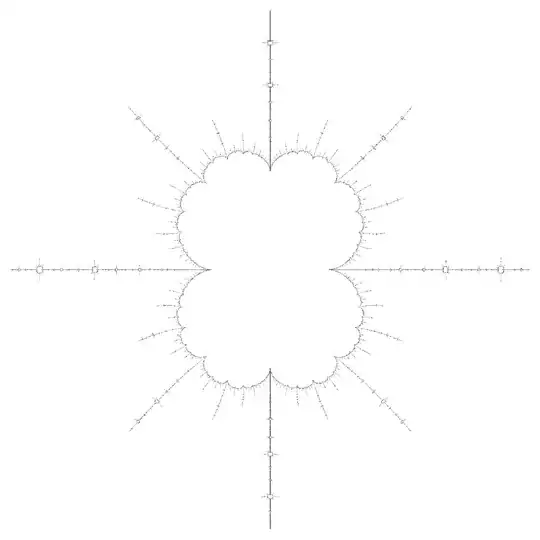
EDIT: As pointed out by Zach Effman, there seem to be a fractal structure emerging from this problem. To better visualize it, I looked at the boundedness of the sequence $\{g_n(z)\}$ for $z\in\mathbb{C}$. More precisely, I made a grid of points $z\in\mathbb{C}$, colored black if $\{|g_n(z)|\}$ is bounded at $z$ and the more quickly $\{|g_n(z)|\}$ diverges to infinity the more white the pixel is. A dramatic fractal structure emerges:
 Does anybody recognize this fractal? Is this a known fractal?
Does anybody recognize this fractal? Is this a known fractal?
The center of this picture reveals a very nice structure:

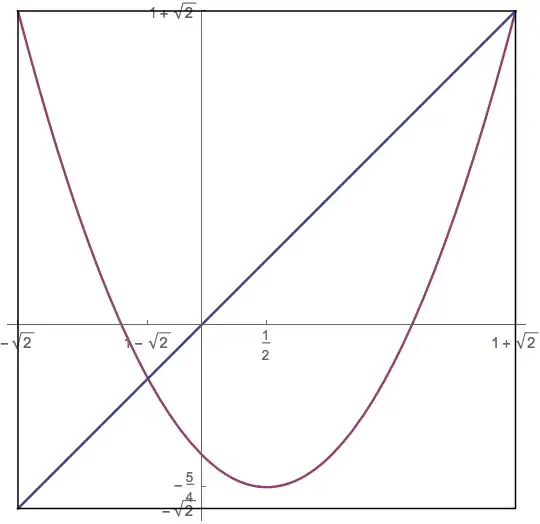
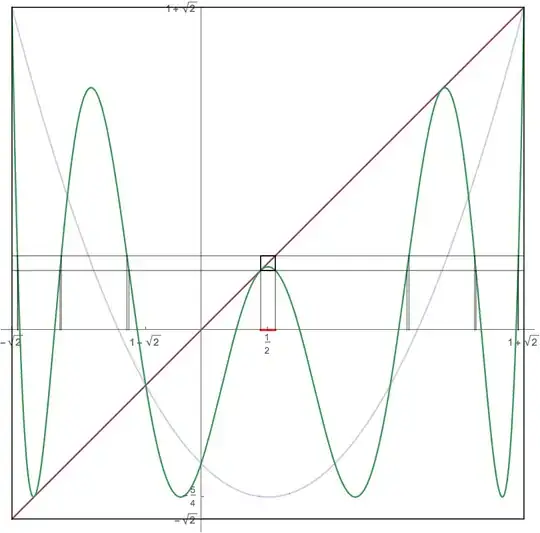


18/100, but after the 6th iteration, the numerator and denominator were both 890750 digits long! – Greg Hurst Dec 26 '14 at 05:44