Extending the zeta function to semiprimes, etc.

Question

The Riemann Zeta function is defined for $s > 1$ as

\begin{align} &\prod _{n=1}^{\infty}\dfrac{1}{1 -\ p_{n}^{\ \ -s}}\\ \end{align}

It is possible to extend the zeta function to semiprimes with

\begin{align} &\prod _{n=1}^{\infty}\dfrac{1}{1 -\ q_{n}^{\ \ -s}}\\ \end{align}

where $q$ runs through the semiprimes $4,6,9\ldots$

and similarly, for all almost primes. Below is a plot of the zeta functions for the k-almost primes $1\leq k\leq 6$:

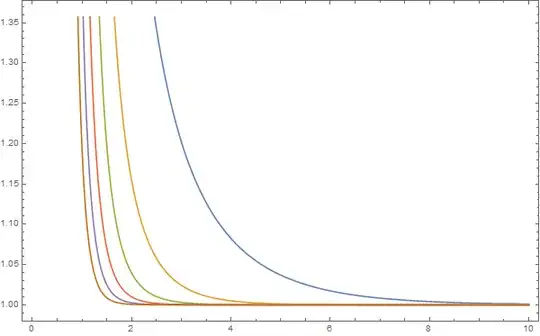
I suspect these functions are rather difficult to approach analytically. Interestingly though, it appears that $\zeta(2s)$ bounds the semiprime zeta function from below:

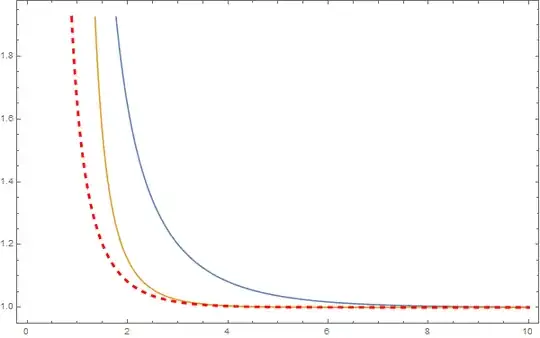
and so on, though the bound gets progressively weaker ... is this likely to be a true statement?

\begin{align} &\prod _{i=1}^n \frac{1}{\left(1-p_i{}^{1-c s}\right)^{c}} \end{align}

with $c=e+k-2$ is closer (though not a lower bound). For $k=2$ (ie semiprime zeta):

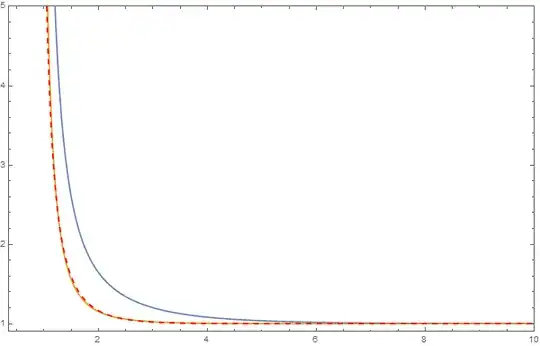
The reciprocals of k-almost primes have been studied by Richard J. Mathar (given in the link in the OEIS sequence here), but I am not aware of any references to the extended zeta functions as outlined above. I would be grateful if anyone knows of any research in this area, or could shed any further light on these functions.

Answer 1

The short answer is yes, there are analogous series (and products).

An early version of this inquiry can be found in Landau. At page 570 (vol.II) of Handbuch der Lehre von der Verteilung der Primzahlen he introduces $\lambda(n)$ and on page 618 introduces the equality

$$\sum\frac{\lambda(n)}{n^s} = \prod(1 + 1/p^s)^{-1} = \frac{\zeta(2s)}{\zeta(s)}$$

in which $\lambda(n) = (-1)^{\Omega(n)}$ and $\Omega(n)$ is the number of prime factors of a number including repetitions. The connection with the Euler product is clear, and while Landau is dealing with odd numbers of factors versus even, the germ of the idea of classes according to numbers of divisors is present here.

The paper in the comments, On the Residue Class Distribution of the Number of Prime Divisors of an Integer, Coons and Dahmen, Nagoya Math j. 202, 2011, 15-22 [Coons], deals with residue classes based on number of prime divisors, so it is also relevant.

Note that the equality (1) in [Coons] is straight out of Landau and the authors establish a result analogous to a well-known result for primes in arithmetic progressions (Theorem 1.1, see also Apostol, ch. 7).

The generalization of sums in [Coons] is essentially what you are asking about and so the answer to your question is yes. The precise form of their sums is due in part to the result they are trying to show. You are using the product but if you look at sums and consider ways to count terms using arithmetic functions in the numerator you get results along the lines of those in the paper.

As a guess, there are historical reasons for the relative wealth of papers on sums of reciprocals of primes of the form $an+b$ over those dealing with numbers of prime divisors. Dirichlet's early success with arithmetic sequences spurred much research and we have a Riemann-like hypothesis for Dirichlet series.

This material is covered in Apostol, Introduction to Analytic Number Theory and your products/sums fall under the general heading of Dirichlet series.

Landau relates his sum to the ratio of $\zeta$ functions above so there is plenty that is known about the behavior of at least some of these.

Will update as time allows. Hope this helps.