7

I'm trying to solve this PDE using Feynman-Kac formula
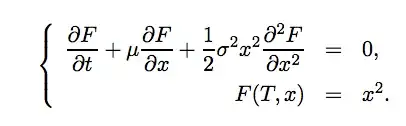
enter image description here

Now i follow the regular steps

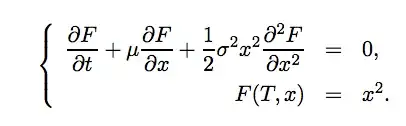
enter image description here

Here is where I don't know how to proceed. How do I calculate this expectation?

Carl
  • 71
  • 1
  • 2
  • Well, I would say that $F(t,x) = \mathsf E_{(t,x)}[X^2_T]$ is the starting point. You've a found a correct SDE: $$ \mathrm dX_t = \mu\mathrm dt + \sigma X_t \mathrm dB_t. $$ Now, to compute expectation try to derive ODEs for first and second moments. – SBF Dec 12 '14 at 10:47
  • @Ilya Convert to integral equation and then take expectation? – BCLC Dec 12 '14 at 11:09

1 Answers1

1

As I've mentioned in the comment, just use the SDE that you derived to obtain ODEs for the moments of $X_T$. That is, let $m(t) = \mathsf EX_t$, then $\mathrm dm_t = \mu\mathrm dt$. A similar equation you can derive for $v(t) = X^2_t$ using Ito's lemma. That's pretty much it.

Edit: you will get the following SDE $$ \mathrm dX^2_t = (2\mu X_t +\sigma^2 X_t^2)\mathrm dt + 2 \sigma X^2_t\mathrm dB_t $$ so that $$ d v(t) = (2\mu m(t) + \sigma^2 v(t) )\mathrm dt $$ and if you've found $m(t)$ as I suggested above, you just need to solve this simple ODE for $v$. Since it is non-homogeneous, you can e.g. use Lagrange method of variating the constant.

SBF
  • 36,568
  • Thank you for the reply but I'm still not sure what to do. Should try to calculate the SDE for Z=X^2 and then somehow reach the answer? – Carl Dec 16 '14 at 08:23
  • @Carl: exactly. – SBF Dec 16 '14 at 08:24
  • Because I then have this equation: first the SDE:
    dZ=2Xdx+sigma^2X^2dt = (sigma^2X+2mu)Xds+2X^2sigma dB I take the integral and expectation and but I don't know how to proceed. I get both Z and X in the equation.
    Sorry If the calcualtion are hard to see but I don't now how to format the text better     – Carl Dec 16 '14 at 08:30