STATEMENT: A dolphin is a special chess piece that can move one square up, OR one square right, OR one square diagonally down and to the left. Can a dolphin, starting at the bottom-left square of a chessboard, visit each square exactly once?
QUESTION: How would one approach this type of problem. It seems that whatever way the dolphin moves the maximum moves always involve the dolphin to traverse an 6x8 square.
Hint: Instead of the usual black/white pattern, color the square $(a,b)$ either green, blue, or yellow, according to the remainder of $a+b$ (mod $3$). Each color forms a diagonal stripe going from the upper left to the lower right, with the stripe pattern going green, blue, yellow, $\dots$ as you move up or to the right. Think about how this coloring relates to a Dolphin's movement, and what a tour of the board would look like in terms of these colors.
Addendum: For your viewing pleasure:
In response to Mike Earnest's question regarding the existence of a Dolphin Tour from alternate starting points: If we started at a blue square, say for example the bottom right corner instead,
The punchline of the proof is that there are in fact 21 yellow, 21 green, and 22 blue squares. Any sequence of moves will be (...,green,yellow,blue,...) repeated. Having started from a green square, after reaching the 21st blue, you will no longer have another green square to go to, and so you cannot continue until reaching the 22nd blue.
In a similar fashion, it is then impossible to reach every square having started at a yellow square either.
Having started at a blue however, as shown above, can be possible (depending on the square), and if is impossible for a specific starting square, would require a different argument.
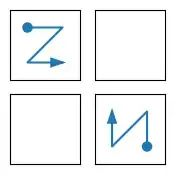
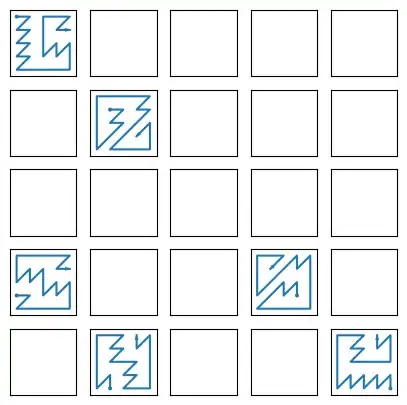
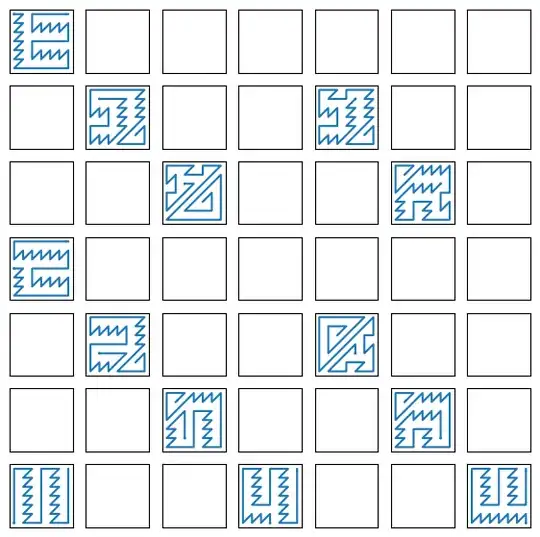
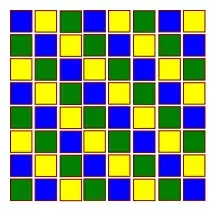
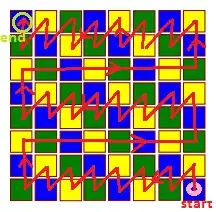
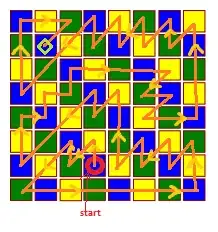
Here are all the starting points which would allow for a complete dolphin tour, with examples (these are not unique) of such tours for each one.
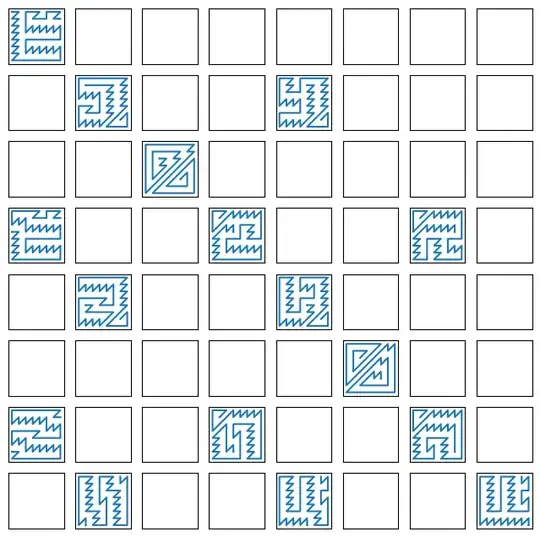
These solutions were obtained by exhaustively searching tours, starting from the blue cells in Mike's answer, using a simple depth-first search. One can speedup the process by noting the symmetry across the bottom-left / top right diagonal, and stopping the search when some cells become unattainable. Here is the python code which was used:
import numpy as np
import matplotlib.pyplot as plt
from enum import Enum
class Moves(Enum):
UP = (0,1)
RIGHT = (1,0)
DOWNLEFT = (-1,-1)
class State:
def init(self, grid, pos, moves=[]):
self.size = 1
for s in grid.shape:
self.size *= s
self.grid = grid
self.pos = pos
self.moves = moves
@classmethod
def new(cls, size, init_pos):
state = np.full((size,size), True)
state[init_pos] = False
return cls(state, init_pos)
def is_done(self):
return len(self.moves)+1 == self.size
def is_impossible(self):
if len(self.moves) == 0:
# Check if the starting point is in a "blue" cell
cnts = [0,0,0]
for i,j in np.ndindex(self.grid.shape):
cnts[(i+j)%3] += 1
i,j = self.pos
for c in cnts:
if c > cnts[(i+j)%3]:
return True
# Check if the last move did block a cell
for dx,dy in ((-2,-1),(-1,-2),(-1,1),(1,-1),(2,1),(1,2)):
x,y = (self.pos[0]+dx,self.pos[1]+dy)
if self.is_valid((x,y)):
blocked = True
for move in Moves:
npos = (x-move.value[0], y-move.value[1])
if self.is_valid(npos):
blocked = False
break
if blocked:
return True
return False
def is_valid(self, pos):
for v in pos:
if v < 0 or v >= len(self.grid):
return False
return self.grid[pos]
def plot(self, ax, *args, **kwargs):
start = self.pos
coords = [start]
for m in self.moves[::-1]:
start = tuple(s-d for s,d in zip(start,m.value))
coords.append(start)
nx,ny = self.grid.shape
ax.set_xlim(-0.5, nx-0.5)
ax.set_ylim(-0.5, ny-0.5)
ax.set_aspect("equal")
dr = self.moves[-1].value
ax.add_patch(plt.Circle(coords[-1], 0.15))
ax.arrow(*(p-0.1*dp for p,dp in zip(self.pos, dr)), *(0.2*p for p in dr),
shape='full', lw=0, length_includes_head=True,
head_width=0.3)
return ax.plot(*zip(*coords[::-1]), *args, **kwargs)
def move(self, move):
newpos = tuple(x+dx for x,dx in zip(self.pos,move.value))
if self.is_valid(newpos):
newgrid = self.grid.copy()
newgrid[newpos] = False
return self.__class__(newgrid, newpos, self.moves+[move])
return None
def avail_moves(self):
avail = {}
for move in Moves:
moved = self.move(move)
if moved is not None:
avail[move] = moved
return avail
def find_solution(self):
if self.is_done():
return self
if self.is_impossible():
return None
for move,res in self.avail_moves().items():
sol = res.find_solution()
if sol is not None:
return sol
return None
def make_sym(self):
def tr(c):
a,b = c
return b,a
tr_m = {
Moves.UP : Moves.RIGHT,
Moves.RIGHT : Moves.UP,
Moves.DOWNLEFT : Moves.DOWNLEFT,
}
return State(self.grid.T, tr(self.pos), [tr_m[m] for m in self.moves])
def plot_grid(n):
fig, axes = plt.subplots(n,n, sharey=True, sharex=True, figsize=(n,n))
for i in range(n):
for j in range(i+1):
ax = axes[-j-1][i]
ax_t = axes[-i-1][j]
ms = State.new(n,(i,j))
sol = ms.find_solution()
if sol:
print("{} -> Found".format((i,j)))
sol.plot(ax)
if i != j:
sol.make_sym().plot(ax_t)
else:
print("{} -> Not found".format((i,j)))
ax.set_aspect("equal")
ax_t.set_aspect("equal")
ax.set_xticks([])
ax.set_yticks([])
plot_grid(8)
plt.show()
To be exhaustive, and as there are some nice patterns, here are the solutions for smaller boards:
