System of nonlinear equations that leads to cubic equation

Question

The system of equations are: $$\begin{align}2x + 3y &= 6 + 5x\\x^2 - 2y^2 - (3x/4y) + 6xy &= 60\end{align}$$

I can solve it through substitution but it is an arduous process to reach this cubic equation:

$$20x^3 + 56x^2 - 243x - 544 = 0$$

And I can only solve this using a computer.

Is there a simpler method?

edit: turns out there was a printing error that made the problem much harder. I posted the actual problem below if you want to see it.

edit 2: The actual problem is far less interesting, but I included it for completeness. There are some really great answers to the above "incorrect" problem however that are definitely worth a read. Thanks everyone for contributing.

Answer 1

Wolfram gives two complex and one real root: $$x=\frac{1}{30}(-28 - \frac{2861}{\sqrt[3]{{498338}+75\sqrt{48312705}}}+\sqrt[3]{{498338}+75\sqrt{48312705}}),$$ which shows that there is no easy way, but following the Cardano method.

Answer 2

There was an error in the question. As I mentioned, this was a from a high school textbook that did not allow for the use of computational software (or even a calculator). The question was from a poor-quality photocopy and the student thought an addition sign was a division sign.

This was what the student told me the question was: \begin{align} 2x + 3y &= 6 + 5x\\ x^2 - 2y^2 - 3x ÷ 4y + 6xy &= 60 \end{align} This is what the question actually was: \begin{align} 2x + 3y &= 6 + 5x\\ x^2 - 2y^2 - 3x + 4y + 6xy = 60 \end{align} Solving and substituting this leaves you with: $$ x^2 + x - 12 = 0 $$ and it is trivial to show that the solutions are then $(3,5)$ and $(-4,-2)$.

If anyone is interested in a further challenge, the textbook hints that there is a more elegant solution than this (this is one of the things that confused me in the first place).

Answer 3

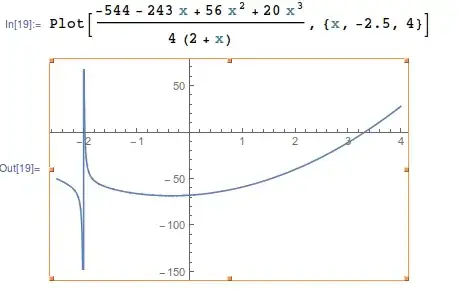
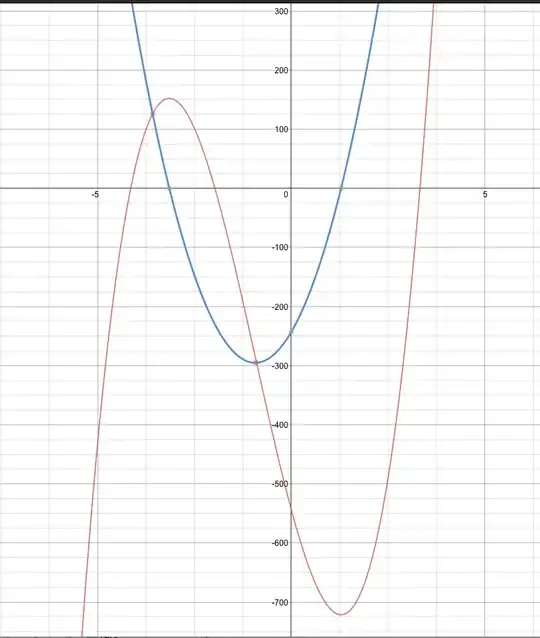
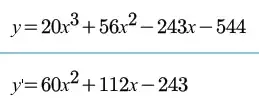$$2x + 3y = 6 + 5x$$$$x^2 - 2y^2 - \frac{3x}{4y} + 6xy = 60$$

Let $\chi=17x+5$ and $\gamma=17y-29$
Then $x=\frac1{17}\!\left(\chi-5\right)$ and $y=\frac1{17}\!\left(\gamma+29\right)$

$$ \frac2{17}\!\left(\chi-5\right) + \frac3{17}\!\left(\gamma+29\right) = 6 + \frac5{17}\!\left(\chi-5\right) $$ $$ \left(\frac1{17}\!\left(\chi-5\right)\right)^2 - 2\cdot\left(\frac1{17}\!\left(\gamma+29\right)\right)^2 - \frac{\frac3{17}\!\left(\chi-5\right)}{\frac4{17}\!\left(\gamma+29\right)} + 6\left(\gamma+29\right)\!\!\left(\chi-5\right) = 60 $$

By expanding, collecting terms and multiplying with constants these can be quite easily be changed into

$$ \gamma=\chi $$ $$ \frac{\chi^2}{289} - \frac{2\gamma^2}{289} +\frac{50276\chi}{289} - \frac{8554\gamma}{289} - \frac{3\chi-15}{4\gamma+116} + 6\chi\gamma-\frac{253087}{289} = 60 $$

Since $\gamma=\chi$ we can subtitute one for another, to avoid confusion I will now use $\lambda=\gamma=\chi$. This also reduces the equation to $\lambda=\lambda$ which reduces this to single equality.

$$ \frac{1733\lambda^2}{289} + \frac{41722\lambda}{289}-\frac{3\lambda-15}{4\lambda+116} = \frac{270427}{289} $$

I'm tired of 289

$$ 1 733\lambda^2 + 41 722\lambda-\frac{867\lambda-4 335}{4\lambda+116} = 270 427 $$

Multiply with $4\lambda+116$

$$ 6 932\lambda^3+367 916\lambda^2+3 757 177\lambda-31 373 867=0 $$

Divide with $6 932$

$$ \lambda^3+\frac{91 979\lambda^2}{1 733}+\frac{3 757 177\lambda}{6 932}-\frac{31 373 867}{6 932} = 0 $$

Subtitute $\lambda=v-\frac{91 979}{5 199}$

$$ \left(v-\frac{91 979}{5 199}\right)^3+\frac{91 979\left(v-\frac{91 979}{5 199}\right)^2}{1 733}+\frac{3 757 177 \left(v-\frac{91 979}{5 199}\right)}{6 932}-\frac{31 373 867}{6 932} = 0 $$

Expand this and divide with $36 039 468$

$$ v^3 - \frac{14 306 982 541}{36 039 468}v - \frac{427 215 759 480 560}{140 526 895 599} = 0 $$

A wild large numbers appear.
Darksonn used variables, it's super effective.

$$p=-\frac{14 306 982 541}{36 039 468}$$ $$q=-\frac{427 215 759 480 560}{140 526 895 599}$$

$$ v^3 + pv + q=0 $$

Perform the substitution $v=w-\frac p{3w}$

$$ \left(w-\frac p{3w}\right)^3+pw-\frac{p^2}{3w}+q=0 $$

Expand the equation

$$ w^3 - \frac{p^3}{27w^3} + q = 0 $$

Let $u=w^3$ and multiply by $u$

$$ u^2 + qu - \frac{p^3}{27} = 0 $$

We pick one of the roots, in the end it dosen't matter which one. If you don't believe me, try yourself.

$$ u=\frac1{18}\left(\sqrt 3\cdot \sqrt{4p^3+27q^2} - 9q\right) $$

Substitute back $w^3=u$

$$ w^3=\frac1{18}\left(\sqrt 3\cdot \sqrt{4p^3+27q^2} - 9q\right) $$

Take the three square roots

$$ w_1=-\frac{\sqrt[3]{\sqrt{12p^3+81q^2} - 9q}}{\sqrt[3]{2} \cdot 3^{2/3}} $$ $$ w_2=\frac{\sqrt[3]{\sqrt{12p^3+81q^2} - 9q}}{\sqrt[3]{2} \cdot 3^{2/3}} $$ $$ w_3=\frac{(-1)^{2/3}\cdot \sqrt[3]{\sqrt{12p^3+81q^2} - 9q}}{\sqrt[3]{2} \cdot 3^{2/3}} $$

In the following, the symbol $w$ denotes any of the $3$ values above

We wan't to invert $v=w_?-\frac 9{3w_?}$, so we get

$$ w=\frac12\cdot\!\left(v\pm\sqrt{v^2+12}\right) $$

This is also written as

$$ v=\frac{w^2-3}w $$

We know that $v=\lambda+\frac{91979}{5199}$

$$ \lambda=\frac{w^2-3}w-\frac{91979}{5199} $$

Substitute in for $w,p,q$

$$ \lambda=\frac{\left(3^{\frac{1}{3}} 2^{\frac{2}{3}} {\left(9 \cdot 3^{\frac{1}{3}} 2^{\frac{2}{3}} - {\left(\frac{3}{12013156} \, \sqrt{3} \sqrt{-11345297051245155823} + \frac{427215759480560}{15614099511}\right)}^{\frac{2}{3}}\right)}\right)}{6 \, {\left(\frac{3}{12013156} \, \sqrt{3} \sqrt{-11345297051245155823} + \frac{427215759480560}{15614099511}\right)}^{\frac{1}{3}}} - \frac{91979}{5199} $$ $$ \lambda=\frac{\left(3^{\frac{1}{6}} 2^{\frac{1}{3}} \\{\left(3^{\frac{2}{3}} 2^{\frac{1}{3}} {\left(15597 \, \sqrt{-34035891153735467469} + 1708863037922240\right)}^{2} - 70214429819350206466848\right)}\right)}{374738388264 \, {\left(15597 \, \sqrt{-34035891153735467469} + 1708863037922240\right)}} - \frac{91979}{5199} $$ $$ \lambda=\frac{\left(3^{\frac{1}{6}} 2^{\frac{1}{3}} {\left(3^{\frac{2}{3}} 2^{\frac{1}{3}} {\left(15597 \, \sqrt{-34035891153735467469} + 1708863037922240\right)}^{2} - 70214429819350206466848\right)}\right)}{374738388264 \, {\left(15597 \, \sqrt{-34035891153735467469} + 1708863037922240\right)}} - \frac{91979}{5199} $$

At this point these values become so ugly they don't even fit on the answer area, so I'll leave doing the last simple substitution as an exercise for the reader.

Answer 4

The first equation simple becomes $y = 2 + x$. In Mathematica (it isn't arduous) do

In[11]:= y = 2 + x;
FullSimplify[x^2 - 2 y^2 - ((3 x)/(4 y)) + 6 x*y - 60]

Out[12]= -68 + x (4 + 5 x - 3/(4 (2 + x)))

In[13]:= Together[-68 + x (4 + 5 x - 3/(4 (2 + x)))]

Out[13]= (-544 - 243 x + 56 x^2 + 20 x^3)/(4 (2 + x))

Line 13 equals zero so you have the desired results.

Even simpler is combing line 11 and 13 so it reads

y = 2 + x;
Together[FullSimplify[x^2 - 2 y^2 - ((3 x)/(4 y)) + 6 x*y - 60]]

For solutions, run NSolve

In[14]:= NSolve[(-544 - 243 x + 56 x^2 + 20 x^3)/(4 (2 + x)) == 0, x]

Out[14]= {{x -> -4.14829}, {x -> 3.32205}, {x -> -1.97376}}

Solution with Solve

In[16]:= FullSimplify[
 Solve[(-544 - 243 x + 56 x^2 + 20 x^3)/(4 (2 + x)) == 0, x]]

Out[16]= {{x -> Root[-544 - 243 #1 + 56 #1^2 + 20 #1^3 &, 3]}, {x -> 
   Root[-544 - 243 #1 + 56 #1^2 + 20 #1^3 &, 1]}, {x -> 
   Root[-544 - 243 #1 + 56 #1^2 + 20 #1^3 &, 2]}}

Plot of rational equation and plot of cubic only:

Answer 5

I did it on paper like so:

reduce the first equation: $$ y = 2 + x $$

substitute: $$ x^2 - 2(2+x)(2+x) - (3x/4(2+x)) + 6x(2+x) = 60 $$

expand: $$ x^2 - 2x^2-8x-8 - 3x/(4x+8) + 6x^2+12x = 60 $$

reduce: $$ 5x^2 + 4x - 8 - 3x/(4x+8) = 60 $$

multiply all terms by (4x+8): $$ 5x^2(4x+8) + 4x(4x+8) - 8(4x+8) - 3x = 60(4x+8) $$

reduce again: $$ 20x^3+40x^2 + 16x^2+32x - 32x-64 - 3x = 240x+480 $$

and reduce one more time: $$ 20x^3 + 56x^2 - 243x - 544 = 0 $$

Answer 6

The first derivative gives a nice view of the inflection points, and clearly shows we are aiming for 3 real roots.

I would bet that the first equation you showed is a typo, as it simplifies too easily. It seems to me they were aiming for an equation that could be solved by algebraic manipulation.

Answer 7

I guess the error is in the question. What if the real first equation was: $$2x+3y=y+5x $$

Which will lead to a simple equation of degree 2, with a nice value of x. $$\sqrt{11}$$

Answer 8

Consider this form of the equation $x^3+\frac{56}{20}x^2+\frac{243}{20}x−\frac{544}{20}=0$ and let's write it as: $$x^3+a_2x^2+a_1x^1+a_0=0. \qquad \text{(Eq1)}$$ Now consider this form of the 3-rd degree characteristic polynomial where the roots are easily discernible: $(x+\alpha)(x+\beta)(x+\gamma) = 0$. Lets transform it, by simple multiplication, to the form of (Eq1):
$(x+\alpha)(x^2+(\beta+\gamma)x+ \beta\gamma) = 0$
$x^3+(\beta+\gamma)x^2+\beta\gamma\ x + \alpha x^2 + \alpha(\beta+\gamma)x + \alpha\beta\gamma = 0$
and finally: $$x^3 + (\alpha + \beta + \gamma)x^2 + (\alpha\beta + \beta\gamma + \gamma\alpha) x + \alpha\beta\gamma = 0 \quad \text{(Eq2)}.$$

We know that $\alpha,\,\beta,\,\gamma$ are the roots, and thus the solutions you are looking for, and, from Eq1 and Eq2, we can state:

$$ \alpha+\beta+\gamma = a_2 = \frac{56}{20},$$ $$ \alpha\beta + \beta\gamma + \gamma\alpha = a_1 = \frac{243}{20},$$ $$ \alpha\beta\gamma = a_0 = \frac{544}{20}.$$

Three equations with three unknowns, should be doable by hand.

Answer 9

Fairly straight forward in Python using sympy:

from sympy.solvers import solve
from sympy import Symbol
x, y = Symbol('x'), Symbol('y')
print solve(20*x**3+56*x**2-243*x-544, [x])

Answer 10

The roots are all real:

$x_{1}=-\frac{14}{15}-\frac{\sqrt{4429}.cos\Big(\frac{acot(-f)}{3}\Big)} {15}$,

$x_{2}=-\frac{14}{15}+\frac{\sqrt{4429}.sin\Big(\frac{atan(f)}{3}+\frac{\pi}{3}\Big)} {15}$

$x_{3}=-\frac{14}{15}-\frac{\sqrt{4429}.sin\Big(\frac{atan(f)}{3}\Big)} {15}$

$f=\frac{192158\sqrt{222021105}}{3330316575}$.