How to show that limit of $(x^3+y^3)/(x-y)$ does not exist at origin?

Question

Show that the limit as $(x,y)\to (0,0)$ does not exist for the function $$ f(x,t)=\begin{cases}\frac{x^3+y^3}{x-y},\quad & x\ne y \\ 0,\quad & x=y\end{cases} $$

My solution is below, but it appears to be inconsistent with the problem. What is wrong?

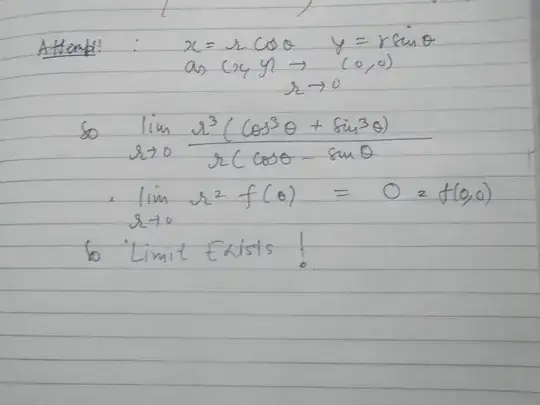
enter image description here

PLEASE AVOID ASKING QUESTIONS ALL IN CAPS ! – Hippalectryon Nov 07 '14 at 18:57 — Hippalectryon, Nov 07 '14 at 18:57
Is this reason for downvoting – godonichia Nov 07 '14 at 19:01 — godonichia, Nov 07 '14 at 19:01

score 4 · Accepted Answer · edited Apr 13 '17 at 12:20

4

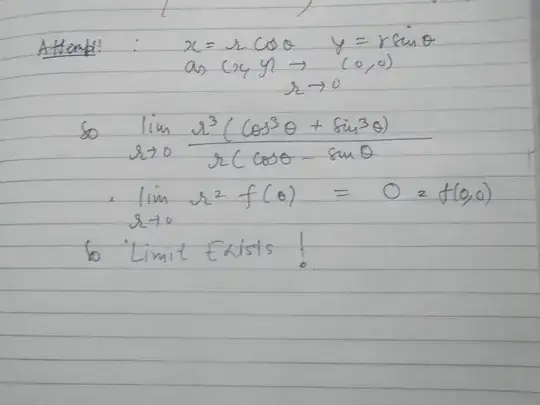
Your conversion to polar coordinates does not prove the limit exists, because in doing so, you are assuming that as $r \to 0^+$, that $\theta$ is a fixed constant with respect to the change in $r$, thus you are only considering a subset of all possible paths tending toward $(0,0)$--specifically, the subset of all straight-line paths to the origin.

See this post for a similar problem, and more information: Limit is found using polar coordinates but it is not supposed to exist.

So, the prove that the limit does not exist, it suffices to discover two distinct paths to $(0,0)$, each suitably parametrized, such that the limit along these paths are unequal to each other.

edited Apr 13 '17 at 12:20

Community

1

answered Nov 07 '14 at 18:56

heropup

143,828

that similar question helped me a lot thanks – godonichia Nov 07 '14 at 19:03
@godonichia Can you help me, with the solution of the problem? What paths did you considered? – Devendra Singh Rana Oct 13 '22 at 12:59

How to show that limit of $(x^3+y^3)/(x-y)$ does not exist at origin?

1 Answers1