0

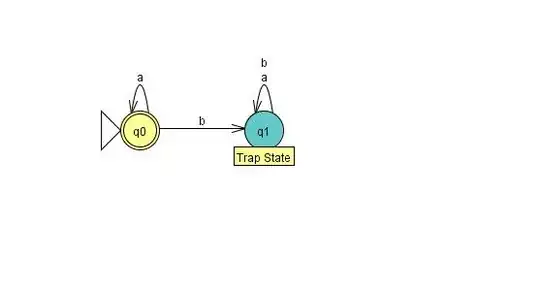
A homework question asks me to a draw a DFA for the regular expression

$((aa^*)^*b)^*$

I'm having trouble with this because I'm not sure how to express the idea of $a$ followed by $0$ or many $a$'s many times, in terms of a DFA.

I would guess it that $(aa^*)^*$ should be the same thing as $\lambda + a^*$ but I'm not sure if I can formally say that. If I could, it would make my DFA simply

Simple DFA

CodyBugstein
  • 3,017
  • 11
  • 31
  • 46

2 Answers2

1

I recommend you first try to understand the language denoted by the regular expression. Once done this can make it easier to build the DFA directly . If you can not think of how to build the DFA you can always turn your regular expression into an NFA and then the NFA into a DFA(Convert regular expression to DFA).

The strings denoted by your regular expression are:

Empty string or a concatenation of strings formed by a chain of zero or more $a's$ followed by a $b$. This mean that your initial state should be a final state too and a word in this language "always"(except $\epsilon$) finish with a letter $b$ so your DFA can't transition to a final state consuming a letter $a$. I hope those hints can help you to generate your DFA directly.

Community
  • 1
Renato Sanhueza
  • 1,345
  • 8
  • 21
1

Edited:

  • (a* a)* can be change to a*
  • Now we have (a* b)*
  • i.e. If nothing comes then, we have to be at final state. If b comes then, we have to be at final state. But if a comes then, sequence of a followed by single b is accepted.

DFA for this will be:

M=({q0,q1}, {a,b}, ∆, q0, {q0})

Where,

q0= initial as well as final state

And ∆: ∆(q0, b)=q0 ∆(q0, a)=q1 ∆(q1, b)=q0 ∆(q1, a)=q1

Explanation: As q0 is initial as well as final, then, epsilon and b is accepted. If a comes then, it will be followed be a b.

user388229
  • 26
  • 2