Clock synchronization in a network with asymmetric delays

Question

Assume a computer has a precise clock which is not initialized. That is, the time on the computer's clock is the real time plus some constant offset. The computer has a network connection and we want to use that connection to determine the constant offset $B$.

The simple method is that the computer sends a query to a time server, noting the local time $B + C_1$. The time server receives the query at a time $T$ and sends a reply containing $T$ back to the client, which receives it at a time $B + C_2$. Then $B + C_1 \le T \le B + C_2$, i.e. $T - C_2 \le B \le T - C_1$.

If the network transmission time and the server processing time are symmetric, then $B = T - \dfrac{C_1 + C_2}{2}$. As far as I know, NTP, the time synchronization protocol used in the wild, operates on this assumption.

How can the precision be improved if the delays are not symmetric? Is there a way to measure this asymmetry in a typical Internet infrastructure?

Answer 1

Inability to measure asymmetry

No, you can't measure the asymmetry. Consider these two communication diagrams, the first with a negative clock offset and equal delays and the second with no clock offset and entirely asymmetric delays (but the same round trip time).

The important thing to notice is that, from the perspective of both the PC and the server, the two interactions are exactly identical. They receive messages at the same time. They send messages at the same time.

You can create more cases by 'grabbing' the PC timeline and 'sliding' it, holding the message send/receive points fixed relative to their respective timelines. The asymmetries you cause are exactly negated by the clock offset. In fact, you can even make messages go BACKWARDS IN TIME one way (as long as the round trip time is still the same) and the server/client STILL can't tell!

Therefore it is impossible to measure latency asymmetries. In the worst case, where you have no information other than that one way latencies are positive and sum to the round trip time, the accuracy of clock synchronization is limited to the round trip time.

Can intermediate infrastructure help?

Whether or not the intermediate infrastructure can help will be heavily dependent upon your theoretical model of the situation.

If the asymmetry is constant and the intermediate infrastructure is the routers on the communication path between you and the server, then no. Even if each router synchronized their clock with the adjacent router, the errors would compound in the same way as if you had synchronized with the server via communication across the routers.

In the real world you can rely on delays being somewhat symmetric for architectural reasons, repeated synchronizations to reduce asymmetry due to queuing delays (etc), and multiple communication paths to reduce other sorts of asymmetry.

If you put your model's assumptions somewhere in between (because it's interesting to explore model space, of course) I expect the result should also be somewhere in between.

Answer 2

Consider a network of time servers known to be synchronous, $\theta = \{A, B, C\}$, and a client machine $P$.

Let $T_{XY}$ be the one way time of flight from machine $X$ to machine $Y$, with the possibility that $T_{XY}\neq T_{YX}$.

Let $\Delta_{XY} = |T_{XY} - T_{YX}|$ be the measure of the asymmetry between machine $X$ and $Y$.

Now, consider that the asymmetry between two synchronous machines can be measured by having the synchronous machines agree to send a one way message to each other at the same time. The difference in the arrival times is $\Delta$ between those machines, i.e.:

$\Delta_{AB} = |T_{AB} - T_{BA}|$

$\Delta_{BC} = |T_{BC} - T_{CB}|$

$\Delta_{CA} = |T_{CA} - T_{AC}|$

can be measured.

Now consider the time of flight of circuits:

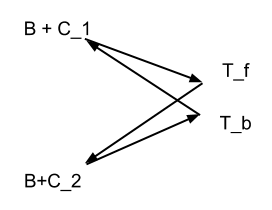
$P \rightarrow A \rightarrow B \rightarrow P$, denoted by $C_{AB}$,

$P \rightarrow B \rightarrow A \rightarrow P$, denoted by $C_{BA}$.

$C_{AB} = T_{PA} + T_{AB} + T_{BP}$

$C_{BA} = T_{PB} + T_{BA} + T_{AP}$

Consider the client machine $P$ to initiate both of these circuits simultaneously, and measures the difference in arrival times, $x$:

$x = C_{AB} - C_{BA} = \Delta_{PA} + \Delta_{AB} + \Delta_{BP}$

Both $x$ and $\Delta_{AB}$ are known by previously mentioned measurements, so moving the unknowns to the left hand side:

$x - \Delta_{AB} = \Delta_{PA} + \Delta_{BP}$

Similarly, for $\{C_{AC}, C_{CA}\}$ and $\{C_{BC}, C_{CB}\}$ it can be shown that:

$y - \Delta_{BC} = \Delta_{PB} + \Delta_{CP}$

$z - \Delta_{CA} = \Delta_{PC} + \Delta_{AP}$

Inspecting carefully, we note that $\Delta_{XY} \equiv \Delta_{YX}$. The left sides contain values known from measurements, the right sides contain 3 unknowns in 3 equations.

Solving simultaneously,

$\Delta_{AP} = \frac{r + s - t}{2}$

$\Delta_{BP} = \frac{r - s + t}{2}$

$\Delta_{CP} = \frac{t - r + s}{2}$

where,

$r = x - \Delta_{AB}$

$s = y - \Delta_{BC}$

$t = z - \Delta_{CA}$

Answer 3

If you only control the endpoints. You can't. See Craig's answer.

Even if you add more machines and a more complex set of computers, like in Bingo's answer, you can reduce to just to machines making the synchronized ones have instantaneous access to the others (delay $T_{XY}$ = 0).

Notice that if you do $T_{AB} = T_{BC} = T_{CA} = 0$, you get $\Delta_{AP} = \Delta_{BP} = \Delta_{CP} = 0$.

So what's wrong? $x = C_{AB}-C_{BA} = \Delta_{PA}+\Delta_{AB}+\Delta_{BP}$

$\Delta_{PA} = |T_{PA} - T_{AP}|$, not $\Delta_{PA} = T_{PA} - T_{AP}$

And if you use the second, then you can not use the assumption $\Delta_{XY} \equiv \Delta_{YX}$ (and if you don't use this, your final equations cancel each other).

So, what can you do? Send a really good clock through mail. ;)

Or, if you have control over all nodes between them, you can check the time to process each packet and calculate the delay between each consecutive pair, that should be symmetrical, if they use the same physical medium both ways.

You may need to account for general relativity, and remember that simultaneity doesn't exist.

Answer 4

NTP actually uses 4 time measurements $t_0, t_1, t_2, t_3$ to compute the "offset". they are the "time points" in the round trip of the packet from client to server back to client but can be regarded as time offsets. its assumed that the time offset can be off between client and server but that both can count local elapsed time offsets accurately.

the client after receiving the return packet has all 4 values and computes the actual offset. once the relative offset is calculated between client and server, the "absolute time" offset can be synchronized ie the client can accurately estimate the servers exact offset measured wrt its local time offset, ie the "delta".

$t_0$ = time [offset] sent at client
$t_1$ = time [offset] recd at server
$t_2$ = time [offset] sent at server
$t_3$ = time [offset] recd at client

the actual formula is $\theta = {(t_1 - t_0) + (t_2 - t_3) \over 2}$

note this formula can handle the case where the time from client to server $t_1 - t_0$ is not the same as from server to client $t_3 - t_2$ (either shorter or longer).

on networks, delay time is due to two major factors, mainly latency and bandwidth.

• latency is the brief delay in routers on sending new [small] packets and is roughly a different constant at each router. it can be measured with the traceroute utility.
• bandwidth is the rate at which large amts of data can be sent eg "upload vs download time" and can also be measured by remote "bandwidth measuring" web sites.

in many modern home/business internet connections the upload rate is much smaller than download rates & this would probably affect the $t_1 - t_0$ vs $t_3 - t_2$ difference whereas latency may be small or somewhat similar between client-to-server and server-to-client.

a basic algorithm to improve accuracy of calculating the offset used in NTP (and can correct for some degree of random network latency) is to repeat the process multiple times and use the "apex of the wedge scattergram". this can be seen on the "clock filter algorithm" on slide 10 of this PPT on NTP by David Mills. see also clock filter algorithm by Mills. (note it can still be employed between a single server and client although the general code is written to allow multiple servers.) this is part of the "mitigation algorithms" described in NTP architecture & algorithms.

Answer 5

If only we could send packets back in time

$$B = T_f + \frac{T_b - T_f}{2} - \frac{C_1 + C_2}{2}$$

Assumptions:

$(B+C_2) - T_b = T_f - (B+C_1)$

$T_f - (B + C_2) = (B + C_1) - T_b$

Answer 6

Here is an idea that sounds absolutely convincing to me and might therefore be absolutely wrong in a dumb way.

Consider the following scenario. We have two nodes $N_1$ and $N_2$ with clocks $C_1$ and $C_2$, respectively. For sake of simplicity, let us assume that the clocks run with the same speed; we denote their difference by $\delta = C_1 - C_2$ which is constant for our purposes. Let us furthermore assume that transmission delays $d_{1 \to 2}$ and $d_{2 \to 1}$ are constant¹.

Have $N_1$ send a message timestamped with $T_1^m$ to $N_2$ and let $T_2^r$ the current time on $C_2$ upon receiving it (do the same for the other direction). In addition, measure round trip time (on either node) $D$ by sending a message back and forth. Now set up this equation system:

$\qquad\begin{align*} T_2^r - T_1^m &= d_{1 \to 2} + \delta \\ T_1^r - T_2^m &= d_{2 \to 1} - \delta \\ D &= d_{1 \to 2} + d_{2 \to 1} \end{align*}$

As this system consists of three equations, has three unknowns and we know there is a solution, it can be solved. Of course the nodes have to exchange their measurements so that they can both compute the same value for $\delta$ (if necessary).

1] I think the assumptions are natural and necessary. They can be justified with the hope that the respective quantities do not change too much for the duration of our synchronisation attempt.