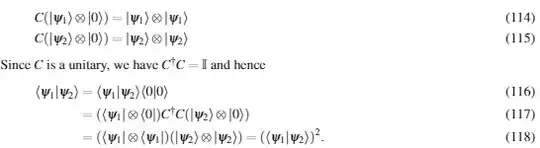For step (116), the equivalence between both of them is proved by
\begin{equation}
(\langle\psi_1|\otimes\langle0|)C^\dagger C(|\psi_2\rangle\otimes|0\rangle) = (\langle\psi_1|\otimes\langle0|)(|\psi_2\rangle\otimes|0\rangle) = \langle\psi_1|\psi_2\rangle\otimes\langle0|0\rangle=\langle\psi_1|\psi_2\rangle\langle0|0\rangle,
\end{equation}
where in the second step I used the property of tensor products that $(A\otimes B)(C\otimes D)=AC\otimes BD$, where obviously the dimensions of the multiplying matrices should match; and for the third step I used the fact that $\langle\psi_1|\psi_2\rangle$ and $\langle0|0\rangle$ are scalars, implying that their tensor product is just a multiplication between them.
For your first question, state $|0\rangle$ is used because it is the typical ancillary system used for quantum algorithms, that is, the zero state is the one used a auxilliary variable for doing the corresponding operations. However, note that the proof is not state dependent, meaning that you can take an arbitrary ancillary qubit, name it $|\rho\rangle$, and prove the theorem. Here I leave you such proof:
\begin{equation}
C(|\psi_1\rangle\otimes|\rho\rangle) = |\psi_1\rangle\otimes|\psi_1\rangle\\
C(|\psi_2\rangle\otimes|\rho\rangle) = |\psi_2\rangle\otimes|\psi_2\rangle
\end{equation}
And so $C$ would be the unitary we are looking for, so now the proof:
\begin{equation}
\langle\psi_1|\psi_2\rangle=\langle\psi_1|\psi_2\rangle\langle\rho|\rho\rangle =(\langle\psi_1|\otimes\langle\rho|)C^\dagger C(|\psi_2\rangle\otimes|\rho\rangle) = (\langle\psi_1|\otimes\langle\psi_1|)(|\psi_2\rangle\otimes|\psi_2\rangle)=(\langle\psi_1|\psi_2\rangle)^2.
\end{equation}
And so the same contradiction as before is obtained, and the theorem is proved.