What happens when I input two qubits starting at state $|00\rangle$ into a hadamard gate?

Question

I was watching the following video https://www.youtube.com/watch?v=IrbJYsep45E
And around 3 minutes in, they do an example computation with two qubits. The qubits started off in the state $|00\rangle$, and then go through what I assume is a Hadamard gate which puts them in a superposition. Why is it a $50\%$ chance of being $|01\rangle$, and a fifty percent chance of being $|10\rangle$? Why is it not a quarter chance of being $|00\rangle$, $|10\rangle$, $|01\rangle$, and $|11\rangle$?

Answer 1

There is a slight misconception in your question. You can't apply a Hadamard gate on $|00\rangle$. Because the basis state $|00\rangle$ is actually a tensor product of a $2\times 1$ dimensional basis state $|0\rangle$ used twice. This results in $|00\rangle = |0\rangle \otimes |0\rangle = \begin{bmatrix}1 \\0\\0\\0\end{bmatrix}$. Now you must take the tensor product of Hadamard gate(which is $2\times 2$ dimensional) too in order to apply it in this state. Like so: $$H \otimes H (|0\rangle \otimes |0\rangle)$$ $$= H|0\rangle \otimes H|0\rangle$$ $$ =\frac{1}{\sqrt{2}}(|0\rangle + |1\rangle) \otimes \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)$$ $$=\frac{1}{2}(|00\rangle + |01\rangle + |10\rangle + |11\rangle)$$. Now obviously $ 4 \times (\frac{1}{2})^2 = 1$, as you have correctly inferred.

Answer 2

It is not two Hadamard gates.
You are 100% correct that two Hadamrd gates would put you in an equal superposition of 00, 01, 10, 11, meaning 25% chance of getting any of those.

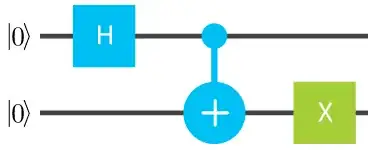
Let's construct her gate based on the input $|00\rangle$ and the output $\frac{1}{\sqrt{2}}\left(|10\rangle +|01\rangle\right)$.

The final state is $|\Psi^+\rangle$ from this question.

So the state can be constructed with this circuit:

where the middle gate is a CNOT.