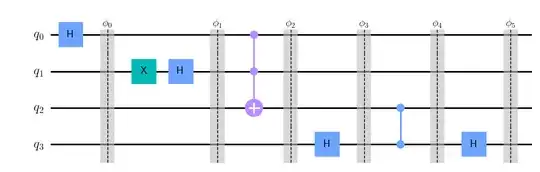
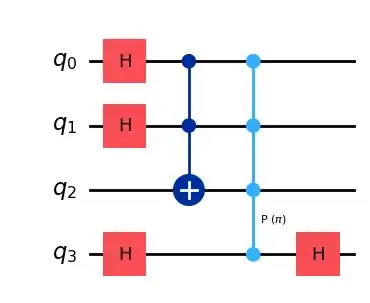
Using the following circuit, I’m trying to do phase kickback to qubit 3, $q_3$, to change its state to $|1\rangle$ when the phase of $|q_2,q_1,q_0\rangle=|111\rangle$ is negative and $|q_3\rangle=|0\rangle$ if it is positive. My goal is to use the sign of the phase coherently, i.e. without measurements, to control further operations in my circuit.
These are the state transitions based on the barriers on the circuit
Case 1
$$\phi_0=\frac{\sqrt{2}}{2}(|0000\rangle + |0001\rangle)$$
$$\phi_1=\frac{1}{2}(|0000\rangle + |0001\rangle - |0010\rangle - |0011\rangle)$$
$$\phi_2=\frac{1}{2}(|0000\rangle + |0001\rangle - |0010\rangle - |0111\rangle)$$
Omitting some terms and focusing on the state(s) of interest
$$\phi_3=… \frac{\sqrt{2}}{4}(-|0111\rangle-|1111\rangle)$$
$$\phi_4=… \frac{\sqrt{2}}{4}(-|0111\rangle+|1111\rangle)$$
$$\phi_5=… \frac{1}{2}(-|1111\rangle)$$
Case 2
Similarly, with positive phase (without X gate in $q1$) attached to $|q_2,q_1,q_0\rangle=|111\rangle$, I’m getting
$$\phi_5=… \frac{1}{2}(+|1111\rangle)$$
For both cases, I’m getting $|q_3\rangle=|1\rangle$.
Question: Is it possible to kickback the phase to an ancilla qubit, $q_3$ in this scenario, and use it coherently to control further operations?
The code to reproduce the above is as below:
from qiskit import QuantumCircuit
from qiskit.quantum_info import Statevector
from matplotlib import rc
Enable mpl rendering in Matplotlib
rc('text', usetex=True)
qc = QuantumCircuit(4)
qc.h(0)
qc.barrier(label="$\phi_0$")
print("phi_0")
sv = Statevector.from_instruction(qc)
display(sv.draw("latex", max_size=100))
Comment this line to get positive phase in |111>
qc.x(1)
qc.h(1)
qc.barrier(label="$\phi_1$")
print("phi_1")
sv = Statevector.from_instruction(qc)
display(sv.draw("latex", max_size=100))
qc.ccx(0, 1, 2)
qc.barrier(label="$\phi_2$")
print("phi_2")
sv = Statevector.from_instruction(qc)
display(sv.draw("latex", max_size=100))
qc.h(3)
print("phi_3")
qc.barrier(label="$\phi_3$")
sv = Statevector.from_instruction(qc)
display(sv.draw("latex", max_size=100))
qc.cz(3,2)
print("phi_4")
qc.barrier(label="$\phi_4$")
sv = Statevector.from_instruction(qc)
display(sv.draw("latex", max_size=100))
qc.h(3)
print("phi_5")
qc.barrier(label="$\phi_5$")
sv = Statevector.from_instruction(qc)
display(sv.draw("latex", max_size=100))
display(qc.draw("mpl"))
EDIT 19/05/2025
To give more context, the goal is to use the phase sign information coherently from the circuit above (which will be a subroutine in my overall circuit) to swap two other qubits,e.g. $q4$ and $q5$, in my circuit, i.e. if the phase is positive, I will swap $q4$ and $q5$, otherwise I don't do anything. It will be a controlled SWAP gate based on the phase information.
The circuit I posted in the question is just a toy circuit that I came out with to convey the problem that I'm facing, so that we can discuss it more easily here.
Also, the first two qubits, $q0$ and $q1$, in the circuit have to be in superposition to reproduce the problem with case 2 reproduced by removing the X gate from $q1$.