Fig. 19 is mainly meant as a toy example to illustrate the difficulty posed by the decoding of a circuit involving a transversal CNOT gate. Thus, Fig. 19(a) is not as deep as it should be for a proper fault-tolerant experiment, but instead corresponds exactly to the syndrome decoding graph of Fig. 19(b).
The results of Fig. 20 were obtained by considering $d$ rounds of stabilizer measurements before and after the transversal CNOT gates (I agree it should have been explicitly stated).
That being said, the main purpose of multiple syndrome extraction rounds is to help with measurement errors. The goal is to not have the error-correcting capabilities of the hindered by syndrome extraction.
You want the most probable cause of logical errors to be $O(d)$ qubit errors aligned along a logical operator, not a few qubit errors hidden by a few measurement errors that more syndrome extraction rounds would have revealed.
Thus, if the measurement error rate is roughly of the same magnitude as the qubit error rate (or below), you need to ensure the syndrome decoding graph as a whole is $O(d)$ deep. Performing $O(d)$ rounds after each transversal gates is sufficient, but it might not be necessary if your circuit includes several of them or your state projection is already deep enough.
To illustrate this last point, consider these two Stim experiments:
import stim
import sinter
import matplotlib.pyplot as plt
Basic memory experiment
def state_preparation(distance, p, syndrome_extraction_round):
circ = stim.Circuit.generated("surface_code:rotated_memory_x", distance=distance,
rounds=3, before_round_data_depolarization=p,
before_measure_flip_probability=p)
final_measurement = circ[-distance**2 // 2 - 2:]
syndrome_extraction = circ[-distance**2 // 2 - 3]
circ = circ[:-distance**2 // 2 - 3]
assert isinstance(syndrome_extraction, stim.CircuitRepeatBlock)
syndrome_extraction = stim.CircuitRepeatBlock(syndrome_extraction_round - 1,
syndrome_extraction.body_copy())
circ.append(syndrome_extraction)
return circ + final_measurement
Modified memory experiment including two transversal Hadamard gates
between each syndrome extraction round
def state_preparation_modified(distance, p, syndrome_extraction_round):
circ = stim.Circuit.generated("surface_code:rotated_memory_x", distance=distance,
rounds=3, before_round_data_depolarization=p,
before_measure_flip_probability=p)
final_measurement = circ[-distance**2 // 2 - 2:]
syndrome_extraction = circ[-distance**2 // 2 - 3]
circ = circ[:-distance**2 // 2 - 3]
assert isinstance(syndrome_extraction, stim.CircuitRepeatBlock), syndrome_extraction
syndrome_extraction = syndrome_extraction.body_copy()
errors = syndrome_extraction[1]
Hs = stim.CircuitInstruction("H", errors.targets_copy())
snippet = stim.Circuit()
snippet.append(Hs)
snippet.append(errors)
snippet.append(Hs)
snippet.append(errors)
snippet += syndrome_extraction
syndrome_extraction = stim.CircuitRepeatBlock(syndrome_extraction_round - 1, snippet)
circ.append(syndrome_extraction)
return circ + final_measurement
if name == "main":
tasks = []
Xs = [0.02 * ((0.05 / 0.02)**(i / 10)) for i in range(11)]
for distance in range(3, 10, 2):
for p in Xs:
circuit = state_preparation(distance, p, distance)
tasks.append(sinter.Task(circuit=circuit, json_metadata={"d": distance, "p": p}))
code_stats = sinter.collect(
num_workers=11,
tasks=tasks,
decoders=["pymatching"],
max_shots=1_000_000,
max_errors=10_000
)
tasks = []
Xs_modified = [0.01 * ((0.03 / 0.01)**(i / 10)) for i in range(11)]
for distance in range(3, 10, 2):
for p in Xs_modified:
circuit = state_preparation_modified(distance, p, distance)
tasks.append(sinter.Task(circuit=circuit, json_metadata={"d": distance, "p": p}))
code_stats_modified = sinter.collect(
num_workers=11,
tasks=tasks,
decoders=["pymatching"],
max_shots=1_000_000,
max_errors=10_000
)
fig, ax = plt.subplots(1, 2)
sinter.plot_error_rate(
ax=ax[0],
stats=code_stats,
x_func=lambda stat: stat.json_metadata['p'],
group_func=lambda stat: stat.json_metadata['d'],
)
ax[0].set_xlim(min(Xs), max(Xs))
ax[0].loglog()
ax[0].legend()
ax[0].set_title("Normal memory experiment")
ax[0].set_xlabel("Phyical Error Rate")
ax[0].set_ylabel("Logical Error Rate per Round")
ax[0].grid(which='major')
ax[0].grid(which='minor')
sinter.plot_error_rate(
ax=ax[1],
stats=code_stats_modified,
x_func=lambda stat: stat.json_metadata['p'],
group_func=lambda stat: stat.json_metadata['d'],
)
ax[1].set_xlim(min(Xs_modified), max(Xs_modified))
ax[1].loglog()
ax[1].legend()
ax[1].set_title("Modified memory experiment")
ax[1].set_xlabel("Phyical Error Rate")
ax[1].set_ylabel("Logical Error Rate per Round")
ax[1].grid(which='major')
ax[1].grid(which='minor')
plt.show()
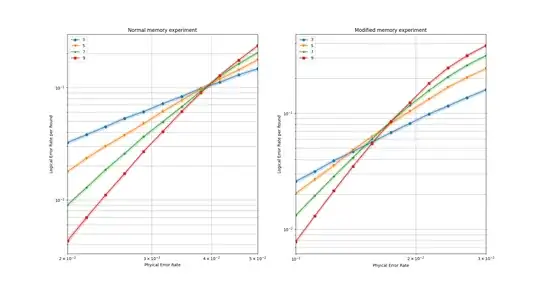
The first is a usual memory experiment, the second inserts two transversal Hadamard gates and depolarizing errors on every data qubits between each syndrome extraction steps (thus only one round of state preparation and one syndrome extraction round after each transversal gate.
The results are similar, the second threshold being roughly two times lower since more error locations of the same rate are considered between each syndrome extraction step.
In a sense, a memory experiment with $O(d)$ rounds of stabilizer measurement is already an experiment with multiple consecutive transversal gates with a single extraction in-between, if one is willing to consider the identity operator as a transversal logical gate.
