What is the circuit that simulates this unitary

Question

What is the circuit that simulates the following unitary matrix?

$$ P = \begin{bmatrix} 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{bmatrix} $$

For context, given a $3$-qubit state $|x\rangle$, this unitary performs the following operation:

$$ P |x\rangle = \begin{cases} |(x+6) \text{ mod } 7 \rangle, & \text{if}\ x < 7 \\ |x\rangle, & \text{otherwise} \end{cases} $$

Answer 1

On second thought, implementing this unitary is a lot simpler than I initially anticipated.

As I mentioned in the comments, this unitary resembles that of a conventional decremeter circuit:

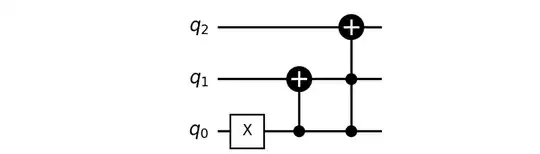
with unitary:

$$ U_{x-1} = \begin{bmatrix} 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{bmatrix} $$

This unitary differs from the one you want in that it maps:

$$ U_{x-1}|000\rangle = |111\rangle \; \text{ and } \; U_{x-1}|111\rangle = |110\rangle $$

but you want:

$$ P|000\rangle = |110\rangle \; \text{ and } \; P|111\rangle = |111\rangle $$

So all you need is to add a $CCX$ gate to flip the least significant bit when the two most significant bits are $1$:

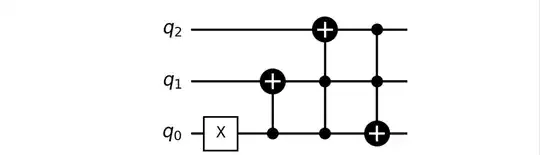
This will give you the unitary you are looking for:

$$ P = \begin{bmatrix} 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{bmatrix} $$