I am trying to simulate the evolution of a three-level system, using mesolve. Strangely, the state seems to "decohere" without any collapse operators involved.
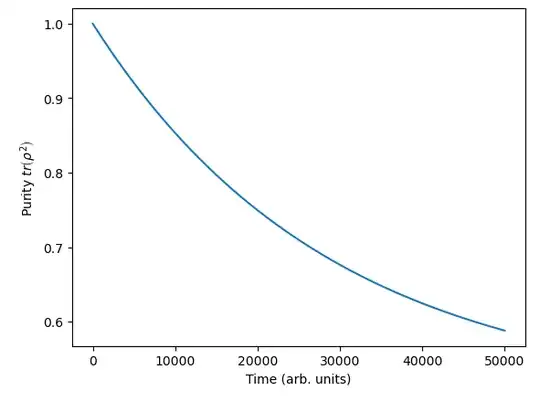
At the moment, I am just trying to calculate the evolution of a superposition state of two of the levels, e.g., $\frac{|0\rangle+|1\rangle}{\sqrt{2}}$, under $H_0 = 2 \pi S_z$. So, while the evolution is unitary, I see the purity of the state decrease. The timescale of decay is ~5e4 periods (i.e., after 5e4 oscillations of the state around the Bloch sphere equator).
I am guessing this is a numerical artifact, but I don't understand it otherwise. I tried playing a bit with the parameters. For example, setting order = 2 seemed to have solved it, but this seems to be just anecdotal and doesn't make sense to me. Playing with the tolerance, as well, seemed to have changed the rate of decay, but I couldn't make sense of its impact on the state.
Obviously, I can evaluate this problem using sesolve (and analytically), but I do intend to introduce collapse operators later on, and I don't want my calculations to be affected by this artifact.
I'd appreciate any input on understanding the root of the issue and solving it.
I'm using qutip 5.0.4, python 3.12.7, on a Macbook Pro (M3), if that has any impact.
A code example:
import numpy as np
import qutip as qu
h0 = 2np.piqu.spin_Jz(1)
psi0 = np.sqrt(1/2)(qu.basis(3,0) + qu.basis(3,1))
rho0 = psi0psi0.dag()
tlist = np.linspace(0,5e4,1234)
result = qu.mesolve(H=h0, rho0=rho0, tlist=tlist,
options=dict(nsteps=1e9, store_states=True))
This is the purity of the state evolution: