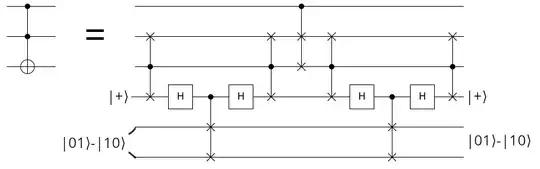
TL;DR: Nope. The triple tensor product of the $+1$ eigenstate of the Hadamard gate is a $+1$ eigenstate of every product of the controlled-SWAP gate and the Hadamard. This is not the case for Toffoli, so Toffoli cannot be approximated as such a product arbitrarily well.
Let $\langle A,B\rangle$ denote the set of unitaries we can obtain by taking all possible finite products of $A$ and $B$ and let $\overline{S}$ denote the closure of $S$ in the topology induced by $\|\,.\|$, i.e. the set of all unitaries that can be approximated arbitrarily well by the unitaries in $S$.
First note that $\text{CCX}\in\overline{\langle \text{CSWAP},H\rangle}$ if and only if $\text{CCZ}\in\overline{\langle \text{CSWAP},H\rangle}$. We will disprove the second statement. Let $|h\rangle:=\alpha|0\rangle+\beta|1\rangle$ denote the $+1$ eigenstate of $H$ and let
\begin{equation}
|hhh\rangle:=|h\rangle\otimes|h\rangle\otimes|h\rangle=\sum_{b\in\{0,1\}^3}\alpha^{3-|b|}\beta^{|b|}|b\rangle\tag1
\end{equation}
where $|b|$ denotes the Hamming weight of the bitstring $b$. The action of $\text{CSWAP}$ on the computational basis is a permutation that preserves the Hamming weight. Therefore, $|hhh\rangle$ is also a $+1$ eigenstate of $\text{CSWAP}$. Consequently, $|hhh\rangle$ is a $+1$ eigenstate of every product in $\langle\text{CSWAP},H\rangle$. Moreover, by continuity of matrix-vector product, $|hhh\rangle$ is a $+1$ eigenstate of every unitary in $\overline{\langle\text{CSWAP},H\rangle}$. But
\begin{align}
\text{CCZ}|hhh\rangle=\text{CCZ}(&\alpha^3|000\rangle+\alpha^2\beta|001\rangle+\ldots+\alpha\beta^2|110\rangle+\beta^3|111\rangle)=\tag2\\
=\,&\alpha^3|000\rangle+\alpha^2\beta|001\rangle+\ldots+\alpha\beta^2|110\rangle-\beta^3|111\rangle\tag3
\end{align}
so $|hhh\rangle$ is not a $+1$ eigenstate of $\text{CCZ}$ and therefore $\text{CCZ}\notin\overline{\langle \text{CSWAP},H\rangle}$.
N.B. it should be possible to use the states appearing in equations $(2)$ and $(3)$ to compute a lower bound on the distance (in some chosen metric) between $\text{CCZ}$ and $\langle \text{CSWAP},H\rangle$.