1

I've been trying to implement the NPA hierarchy in MATLAB using CVX library. To start off with, I thought of finding the bound of CHSH using the first level of NPA hierarchy. I represented my gram matrix as an addition of 2 matrices, One consisting of all the non-negative values and the other consisting of complex values. I believe that I have added all the necessary constraints, but when I'm trying to maximize my objective function, it's giving me an error, saying that it's convex but its maxima is unbounded, which is not the case for CHSH inequality.

cvx_begin sdp
variable T(5,5) nonnegative semidefinite
variable R(5,5) complex semidefinite
X=T+R;
maximize norm(X(4,2)+X(4,4)+X(5,2)-X(5,3)-X(2,1)-X(4,1)+0.5);
subject to
X(1,1)==1;
X>=0;
X==X';
T(1,1)==1;
T==T';
0<=T(2,1)<=1;
0<=T(3,1)<=1;
0<=T(4,1)<=1;
0<=T(5,1)<=1;
0<=T(2,2)<=1;
0<=T(4,2)<=1;
0<=T(5,2)<=1;
0<=T(3,3)<=1;
0<=T(4,3)<=1;
0<=T(5,3)<=1;
0<=T(4,4)<=1;
0<=T(5,5)<=1;
T(3,2)==0;
T(4,3)==0;
T(2,1)==T(2,2);
T(3,1)==T(3,3);
T(4,1)==T(4,4);
T(5,1)==T(5,5)
abs(R(3,2))<=1;
abs(R(5,4))<=1;
R(2,1)==0;
R(3,1)==0;
R(4,1)==0;
R(5,1)==0;
R(2,2)==0;
R(4,2)==0;
R(5,2)==0;
R(3,3)==0;
R(4,3)==0;
R(5,3)==0;
R(4,4)==0;
R(5,5)==0;
R(1,1)==0;
cvx_end

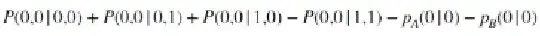
Gram matrix where the rows and columns correspond to the projective operators with respect to a particular input and output for Alice and Bob Gram matrix where the rows and columns correspond to the projective operators with respect to a particular input and output for Alice and Bob. enter image description here

This is the expression that I'm trying to optimize.

Karthik Nambiar
  • 11
  • 2

1 Answers1

2

If all you want is to upper bound CHSH, you can use the short NPA paper. Equation (8) shows the moment matrix you need.

Some specific comments about your code:

  1. Variable $T$ doesn't exist.
  2. In principle $R$ is indeed complex, but it can be chosen to be real without loss of generality, which makes the optimization much faster.
  3. You want the objective and the constraints to be linear, so there's no norm or absolute value.
  4. I have no idea where these constraints are coming from, but they are incorrect. Read the NPA paper to get the correct ones.

If all you want is an implementation of the NPA hierarchy, there are several already available. For MATLAB I'm aware of QETLAB's, which is easy to install but very slow, and Moment (my own project), which is a bit harder to install but is as fast as it gets.

Mateus Araújo
  • 3,167
  • 10
  • 20