Interpretation of a circuit that yields the same result for initializations $|+\rangle$ and $|-\rangle$

Question

How can I interpret a quantum circuit that results in the same state for the initialization $\newcommand{\ket}[1]{|#1\rangle}\newcommand{\bra}[1]{\langle #1|}\ket{+}$ and $\ket{-}$?

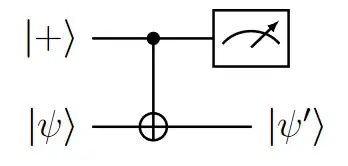
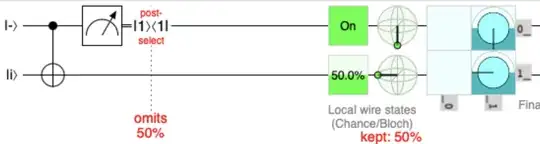
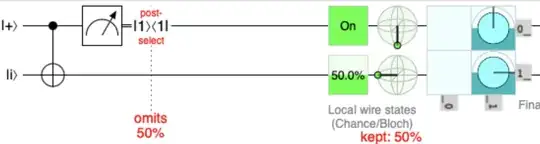
For example, the circuit consisting of a CNOT where the control qubit is measured gives the same result for both initialization states $\ket{+}$ and $\ket{-}$.

In both cases $$\ket{\psi'}=\frac{1}{2}\left(\ket{\psi}\bra{\psi} + X\ket{\psi}\bra{\psi}X^\dagger\right)$$

This is just a simple example. In general the circuit could have multiple ancilla qubits initialized to $\ket{+}$ or $\ket{-}$ and an arbitrary $n$-qubit input state.

Are there any general statements I can make about such circuits?

Answer 1

The way to think about the circuit you showed (and it can generalise to some multi-qubit cases) is that when you measure, you collapse the qubit into a particular state, 0 or 1. You can now run the circuit backwards in time, and it's as if the qubit was in that state at the various steps. So, if you get a 1 measurement outcome, in this case it's like the top qubit was in the $|1\rangle$ state when it controlled the controlled-not, and so that determines what happens to the target qubit. (This works particularly well because the measurement basis and the basis of the control coincide.) So, all that really matters is that for the different possible input states, they have identical probabilities for giving the (tracked-back) measurement outcomes, i.e. $$ |\langle 0|+\rangle|^2=|\langle 0|-\rangle|^2. $$

By that token, for your depicted circuit, arbitrary families of states $\alpha|0\rangle+\beta|1\rangle$ for fixed $|\alpha|^2$ should all give the same output.

Answer 2

One way of seeing this is that the difference between the circuits is a $Z$-gate applied to the first qubit. This won't affect the measurement, and $Z$-gates are not 'transposed' by the CNOT gate to the target qubit, so the circuit results must be identical.

Answer 3

To see why $|+\rangle$ and $|-\rangle$ states are not the same consider $|\psi\rangle = |i\rangle$ and the measurement outputs $|1\rangle$.

The two states only differ by a global phase, but they are not the same.

Instead, the reason why the two initialisations are logically equivalent resides in the measurement. Apply the deferred measurement principle in reverse to notice that the first qubit works like a classical 50/50 bit.