Constructing a block unitary from non-unitary matrices

Question

Background:

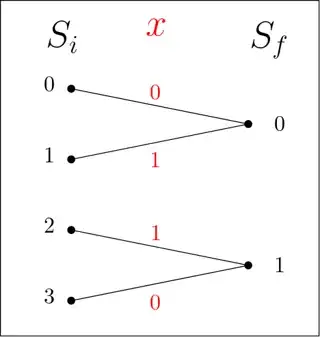
I have a function $f(s_i, s_f, x)$ where $s_i \in \{0,1,2,3\}; \quad x,s_f \in \{0,1\}$ which is defined as:

$$ f(s_i, s_f, x) = \begin{cases} 1, & \text{if } (s_i, s_f, x) \in\{(0,0,0),(1,0,1),(2,1,1),(3,1,0)\}\\ 0, & \text{otherwise} \end{cases} $$

also represented by this image:

The function can also be represented as a family of matrices by choosing a particular set of arguments to index the matrix. For example, one representation (let's call this Rep. 1) is to index the rows by $s_f$ and the columns by $x$, giving a set of matrices parametrized by $s_i$:

$$ \begin{equation} f(s_i, s_f, x)= \begin{cases}{\left[\begin{array}{ll} 1 & 0 \\ 0 & 0 \end{array}\right], s_i=0 \quad ;\left[\begin{array}{ll} 0 & 1 \\ 0 & 0 \end{array}\right], s_i=1} \\ {\left[\begin{array}{ll} 0 & 0 \\ 0 & 1 \end{array}\right], s_i=2 \quad ;\left[\begin{array}{ll} 0 & 0 \\ 1 & 0 \end{array}\right], s_i=3}\end{cases} \end{equation} $$

A second matrix representation (Rep. 2) is using $s_f$ for rows, $s_i$ for columns and parametrised by $x$ as follows:

$$ f(s_i, s_f, x)=\left\{\begin{array}{lll} \left(\begin{array}{llll} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right), & x=0 \\ \left(\begin{array}{llll} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array}\right), & x=1 \end{array}\right. $$

Query:

I want to encode the (non-unitary) matrices in Rep. 1 in such a way that we obtain a block unitary matrix, which can then be represented a gate acting on a quantum circuit.

Any kind of unitary is allowed, (such as encoding in a larger block to obtain some form of a controlled gate) which implements the function $f$, although it would be good if $x$ and $s_f$ are not grouped together in the indexing (since I require $x$ at the 'input' and $s_f$ at the 'output' of the gate)

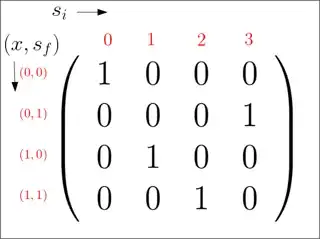
Illustration: As an example of what I am looking for, the matrices in Rep. 2 can be denoted as a unitary by indexing the rows with the ordered pair $(x,s_f)$ and the columns by $s_i$ to obtain the following matrix:

However, as I said, this form does not let me have $x$ as an input to the gate.

Summary: In general, is there any way of encoding the non-unitary projector matrices into a unitary matrix. If not, is there an explanation of why the matrices in Rep. 1 cannot be grouped to obtain a unitary? Personally, I feel that it is not possible to have a unitary encoding which implements the function AND satisfies the restriction on $x$ and $s_f$, since any matrix obtained is sparse with very few non-zero elements. Any help on this is appreciated.

Answer 1

For Rep. 1 you can use a Linear Combination of Unitaries (LCU) for block encoding each of your projections, and then use a control statement according to the the $s_i$ variable. If we designate the four projections by $P_0$, $P_1$, $P_2$, and $P_3$ then: $$ \begin{align} P_0 = 1/2(I+Z),\\ P_1 = 1/2(X+iY),\\ P_2 = 1/2(I-Z),\\ P_3 = 1/2(X-iY), \end{align} $$ where $I$, $X$, $Z$, $Y$ is the Pauli basis. Here is how to code your matrix using Classiq python SDK package:

1. Declare a quantum function that block encodes an equal superposition of two unitaries $\frac{1}{2}(U_1+U_2)$

The following function applies $U_1+U_2$ given that the prepare_qbit is at state 0.

from classiq import *
@qfunc
def lcu2_encoding(select_qfuncs: QCallableList, prepare_qbit: QBit):
    within_apply(
        lambda: H(prepare_qbit),
        lambda: repeat(2,
                       lambda i: control(prepare_qbit==i, lambda: select_qfuncs[i]()
                                        )
                      )
    )

2. Define the four projections using the LCU quantum function

from classiq.qmod.symbolic import pi
@qfunc
def si_0(x: QBit, aux: QBit):
    lcu2_encoding( [lambda: IDENTITY(x), lambda: Z(x)], aux)
@qfunc
def si_1(x: QBit, aux: QBit):
    lcu2_encoding( [lambda: X(x), lambda: (U(0,0,0,pi/2,x), Y(x))], aux)
@qfunc
def si_2(x: QBit, aux: QBit):
    lcu2_encoding( [lambda: IDENTITY(x), lambda: (RY(2*pi,x), Z(x))], aux)
@qfunc
def si_3(x: QBit, aux: QBit):
    lcu2_encoding( [lambda: X(x), lambda: (U(0,0,0,-pi/2,x), Y(x))], aux)

3. Define a function for the full matrix encoding

Here we select each of our four LCUs according the the $s_i$ state (note that each LCU has its own auxiliary):

@qfunc
def my_unitary_encoding(auxs: QArray[QBit], x: QBit, si: QNum):
    repeat(2**si.size,
           lambda i: switch(i, [lambda: control(si==i, lambda: si_0(x, auxs[0])),
                                lambda: control(si==i, lambda: si_1(x, auxs[1])),
                                lambda: control(si==i, lambda: si_2(x, auxs[2])),
                                 lambda: control(si==i, lambda: si_3(x, auxs[3]))]
                           )
          )

The functionality can be verified as follows:

We can define a model in which we initialize the $s_i$ variable to an equal superposition of $|i\rangle$ for $i=0,1,2,3$. Then we can check the value of $x$, given that the auxiliary qubits are at state zero.

@qfunc
def main(auxs: Output[QArray[QBit]], x:Output[QBit], si: Output[QNum]):
    allocate(4,auxs)
    allocate(1,x)
    # X(x) # uncomment here to verify s_i=1,3
    allocate_num(2,False, 0, si)
    hadamard_transform(si)
    my_unitary_encoding(auxs,x,si)
qmod = create_model(main)
qprog = synthesize(qmod)
show(qprog) # for vizualizing the circuit
results = execute(qprog).result()
for sample in results[0].value.parsed_counts:
    if sample.state["auxs"]==0:
        print(sample)

The output after running the above code is:

state={'auxs': 0.0, 'x': 1.0, 'si': 3.0} shots=544
state={'auxs': 0.0, 'x': 0.0, 'si': 0.0} shots=504

As we can see, we do not see results for $s_i=1,2$ as $P_1$, $P_2$ return zero projection for $x=|0\rangle$.

In the attached figure you can see how the circuit looks like. The multi-controlled operations use extra auxiliaries. You can diminish these by changing the preferences of the synthesis (e.g., optimizing the quantum model over width)

(disclaimer: I am currently a Classiq employee).