Stabilizers of the [[12, 2, 4]] "Carbon" code

Question

In a recent experimental paper, Microsoft with IonQ claimed that they demonstrated the "repeated error correction" with both the $[[7, 1, 3]]$ Steane code and the $[[12, 2, 4]]$ "Carbon" code, both of which are self-dual CSS codes.

I am particularly interested in the stabilizer description of the Carbon code, as the code reminds me the recent related work in the many-hypercube codes or the concatenated C4/C6 code. However, I didn't find any explicit description of the code in the original paper.

Does anyone know what on earth the Carbon code looks like? Or is there a way that we could speculate the stabilizer set of the code with the parameter $[[12, 2, 4]]$ and its self-dual property?

Answer 1

TLDR: I find the construction of the code, which can be understood as a special type a 3D color code based on a hexagon nut. Special thanks to @DaftWullie for providing information about the condition of "weak" self-dual.

X check matrix

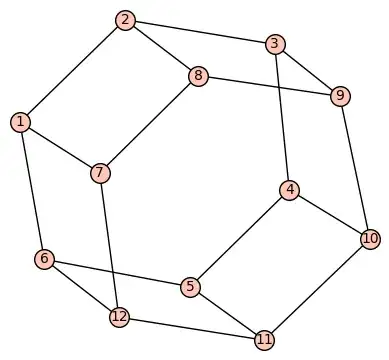
We have five stabilizer generators for each X/Z check so let's start with the $H_X$ first. Looking at the nut, we have two hexagon faces and six rectangular side faces. Two of the $X$ stabilizers are defined on the two hexagon faces. The other three are defined on the adjacent pair of side faces. If I call $S_1$ as the face of qubit $\{1,2,7,8\}$ and $S_2$ as the clockwise next face and so on, The three side-face X stabilizers are separately supported on $S_1 + S_2$, $S_3 + S_4$ and $S_5 + S_6$. The check matrix $H_X$ are therefore given by $$ H_X=\begin{bmatrix}1&1&1&0&0&0&1&1&1&0&0&0\\ 0&0&1&1&1&0&0&0&1&1&1&0 \\ 1&0&0&0&1&1&1&0&0&0&1&1 \\ 1&1&1&1&1&1&0&0&0&0&0&0\\ 0&0&0&0&0&0&1&1&1&1&1&1\end{bmatrix} $$ It's not hard to verify $d_X = 4$.

Z check matrix

If $H_Z = H_X$, we can verify that $$ H_X H_Z^{T}\neq 0, $$ and we need to permute the column of $H_X$ a little in order to find a valid $H_Z$ (permutation doesn't change the distance, so $d_Z=4$ for sure). I use Python code to brutally find possible permutations for $H_Z$, and it seems like there are more than one solution. For example, the permutation index can be $$ (1,2,3,4,5,6,7,8,9,10,11,12)\rightarrow(10, 5, 12, 9, 2, 8, 11, 4, 6, 3, 7, 1) $$ Here is the code I used:

import numpy as np
H_X = np.array([
    [1,1,1,0,0,0,1,1,1,0,0,0],
    [0,0,1,1,1,0,0,0,1,1,1,0],
    [1,0,0,0,1,1,1,0,0,0,1,1],
    [1,1,1,1,1,1,0,0,0,0,0,0],
    [0,0,0,0,0,0,1,1,1,1,1,1]
]
)
result = []
for _ in range(1000000):
    perm_index = np.random.permutation(range(12))
    temp = H_X[:,perm_index].transpose()
    A = H_X @ temp
    if np.any(np.mod(A,2)):
        pass
    else:
        result.append((perm_index,temp))

How I find the hexagon nut

In the original paper, they frequently mentioned that term "automorphism" when discussing the logical opeartion of this code. I then go search for the automorphism group of size $N=12$ and find this post. With the pretty figure of the automorphism in mind, it's then not hard to find the answer by spending some time on brutally placing stabilizer on each plaquette and check the code distance.

Answer 2

I tried to answer this (quickly) but failed. A probable reason is listed at the end of the answer. However, I thought I'd record the attempt in case it assists someone else:

Since the code is self-dual and CSS, we know the parity check matrices satisfy $H_X=H_Z$ and the code properties tell us these must be $5\times 12$ binary matrices. The generators are linearly independent, so I can always choose them in standard form $$ H_X=[I\ A]. $$ I assume that the code is non-degenerate, which means that each column is distinct. The ordering of columns is irrelevant. So, I can search over all sets of size 7 of distinct binary strings of length 5 (to specify $A$). I can ask whether, for a given choice, the resultant $H_X$ satisfies $H_X\cdot H_X^T\equiv 0\text{ mod }2$. If not, discard. This left me with a list of 40 options. However, all had a null space (modulo 2) that contained a length 3 binary string, meaning that the distance of each of those codes is at most 3.

Again, for the record, this is the Mathematica code I used (maybe someone will find a bug):

(*these yield the distinct binary strings*)
opts = Table[
   If[MemberQ[{1, 2, 4, 8, 16}, n], ## &[], n], {n, 3, 2^5 - 1}];
(*iterate through all possible non-degenerate codes*)
out = ParallelTable[
   mat = IntegerDigits[#, 2, 5] & /@ Join[{1, 2, 4, 8, 16}, v];
   If[Total[Mod[Transpose[mat] . mat, 2], 2] == 0, 
    Transpose[mat], ## &[]], {v, Subsets[opts, {7}]}, 
   Method -> "CoarsestGrained"];
(*with the remaining, self-dual, codes, give upper bound on distance*)
Min[Total[Transpose[NullSpace[#, Modulus -> 2]]]] & /@ out

PS codetables.de tells us that there are [[12,2,4]] codes (indeed, [[12,4,4]] codes) which are non-CSS.

Further, the carbon code has already been entered on error correction zoo. Intriguingly, they list the logical Hadamard as being "transversal physical Hadamard followed by a qubit permutation". That implies that they are perhaps stretching the definition of self-dual compared to what I was expecting. It presumably means that $H_X$ and $H_Z$ are only equal up to the permutation of columns. This is something that I didn't account for in my above test.