2

I am trying to replicate this oracle circuitoracle circuit

given in this paper. I am trying to implement a Grover circuit that searches for the key for a known plaintext-ciphertext pair (P,C) = (0xF2,0x14). The oracle circuit for the problem is shown here. I have written a Qiskit code:

#Creating the MAJ gate

qr = QuantumRegister(3)
MAJ = QuantumCircuit(qr)
MAJ.cx(qr[2], qr[1])
MAJ.cx(qr[2], qr[0])
MAJ.mcx([qr[0], qr[1]], qr[2])
MAJ_gate = MAJ.to_gate()


#Creating UMA gate


qr1 = QuantumRegister(3)
UMA = QuantumCircuit(qr1)
UMA.mcx([qr1[0], qr1[1]], qr1[2])
UMA.cx(qr1[2], qr1[0])
UMA.cx(qr1[0], qr1[1])
UMA_gate = UMA.to_gate()


#Creating a n-qubit adder circuit


n = 9
qr = QuantumRegister(n)
adder_ckt = QuantumCircuit(qr)


#Appending MAJ gates


i = 0
while i+2 < n:
adder_ckt.append(MAJ_gate, ([qr[i] for i in range(i, i+3)]))
i = i+2


#Append the CNOT gate
#adder_ckt.cx(qr[n-2], qr[n-1])


#Appending the UMA gates
j = n
while j > 2:
adder_ckt.append(UMA_gate, ([qr[i] for i in range(j-3, j)]))
j = j-2


#Converting to gate
adder = adder_ckt.to_gate()


#Create oracle gate


#Key length
k = 4


#Define Registers
q = QuantumRegister(3*k+1)


#Define the circuit
keyfinder = QuantumCircuit(q)


#Put keys into superposition
for i in range(1, 5):
    keyfinder.x(q[i])
    keyfinder.h(q[i])


#Modify qubits according to plaintext bits

keyfinder.x(q[6])
keyfinder.x(q[i] for i in range(9, 13))


adder_list = []
for i in range(5):
    adder_list.append(i)
for i in range(9, 13):
    adder_list.append(i)


keyfinder.append(adder, [q[i] for i in range(0, 9)])
keyfinder.append(adder, adder_list)


#Middle part of the oracle
for i in range(5,7):
    keyfinder.x(q[i])
keyfinder.x(q[8])
for i in range(10, 13):
    keyfinder.x(q[i])


adder_list2 = [i for i in range(5,12)]


keyfinder.h(q[12])
keyfinder.mcx(adder_list2, q[12])
keyfinder.h(q[12])


for i in range(5,7):
    keyfinder.x(q[i])
keyfinder.x(q[8])
for i in range(10, 13):
    keyfinder.x(q[i])


#Append the adders again
keyfinder.append(adder, adder_list)
keyfinder.append(adder, [q[i] for i in range(0, 9)])

where the MAJ gate is
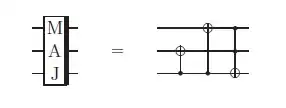
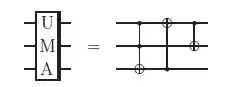
and the UMA gate isenter image description here enter image description here

The adder is a quantum ripple-carry adder. The authors suggest to ignore the high-carry qubit and I have thus done so. My adder turns out to be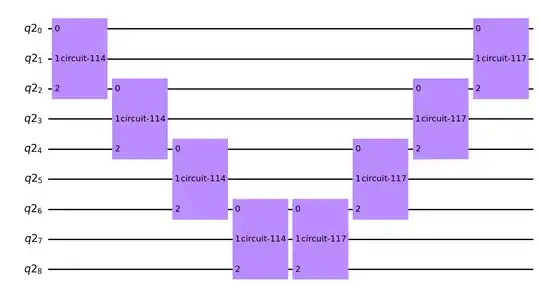enter image description here while my oracle turns out to be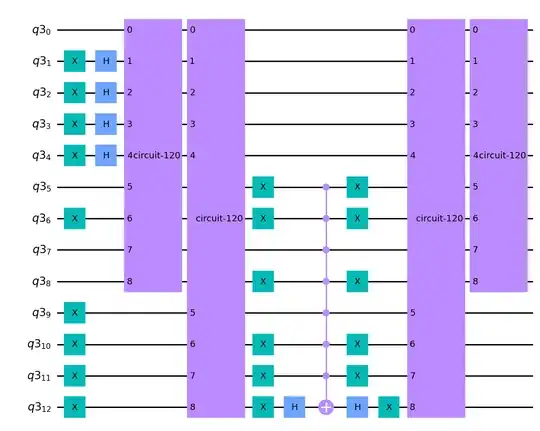enter image description here Now the problem is after iterating the circuit 3 times, I am supposed to get 0010 after making measurements on the keys, but I am getting a wrong answer of 0000. I cannot find the mistake. I would really appreciate if someone helps me out.

abirbhav
  • 43
  • 4

0 Answers0