Recently I am trying to do some simulations on the surface code to get the empirical curve of logical error(P_L) corresponding with physical error rate(p) and code distance(d) as Towards practical classical processing for the surface code do. However, after several rounds of simulation, I found something weird happened in my work. I can't get the result of threshold theorem do! No matter how low the physical error rate is, adding more qubits always introduce more errors.
So I want to know which part of my simulation is wrong.
The following is my simulation route. Let's take d=5 as example.
Step1: First in my program, I will generate a 5*5 lattice of physical qubits. And in each round of stabilizer measurement simulation, I randomly put errors using the standard Depolarizing noise model on each qubits in the lattice, which means every qubits in the lattice will store an information of one of ['I', 'X', 'Y', 'Z'] with the probability [1 - 8p, 8p/3, 8p/3, 8p/3].
Step2: In this step, I perform stabilizer measurement on the measure qubit to get the "-1" syndrome outcome.(Suppose the measure qubit is to measure the "Z" type stabilizer, then one neighbouring physical qubits containing "X" or "Y" will flip the outcome.) Now, I just consider the perfect measurement case to simpilify the simulation. As a consequence, I just need to do one round of stabilizer measurement, and ignore the time boundary.
Step3: Once I get all of the "-1" syndrome in the stabilizer measurement step, I just perform MWPM algorithm using the library of "networkX". And the distance of two stabilizer is defined as the Manhattan distance.
Step4: With all "-1" pairs as the outcome of MWPM, I generate the operators of the qubits in the shortest path of these pairs. And applying these operators is the error correction step.
Step5: After recovering the error. I combined the simulated error in step1 and the recovery operator in step4 to detect if this round of simulation occurs a logical error. If it does, count it. Return to step1.
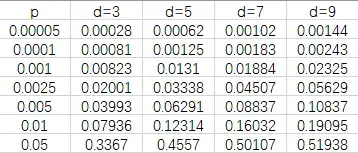
The simulation result of my work is:
I possiblly find out where the problem is. Seems like there are some weird results in the usage of the nx.min_weigh_matching min_weight_matching implemented by the networkX lib.
Here is the proof. The code is running in the python.
import networkx as nx
G = nx.Graph()
edges = [(0, 1, {'weight': 3}), (1, 2, {'weight': 1}), (0, 3, {'weight': 1}), (2, 3, {'weight': 0})]
G.add_edges_from(edges)
print(nx.min_weight_matching(G))
I generate a complete graph of 4 nodes with the above weight. However, the result is:
{(0, 1), (2, 3)}
And the total weight(3) of this matching is larger than the total weight(2) of matching {(0, 3), (1, 2)}.