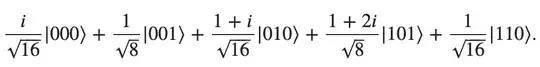2

I do not understand how the initialize function in QiSkit is working. I know that it is used to put a qubit in a specific custom state.

My question is - how is it implemented or how to do such a thing mathematically, which gates to use and why? Hope that my question is clear.

For example: Consider that we have 3 qubits, and I would like to set them in the following state: enter image description here

So to do this using qiskit, I can use the initialize function as following:

import math
desired_vector = [
    1 / math.sqrt(16) * complex(0, 1),
    1 / math.sqrt(8) * complex(1, 0),
    1 / math.sqrt(16) * complex(1, 1),
    0,
    0,
    1 / math.sqrt(8) * complex(1, 2),
    1 / math.sqrt(16) * complex(1, 0),
    0]
initialize_circuit_3q = Q_program.create_circuit('initialize_circuit_3q', [qr], [cr])
initialize_circuit_3q.initialize("init", desired_vector, [qr[0],qr[1],qr[2]])

So I understand how to do this with qiskit, but my question is how this is done theoretically/mathematically, I mean if I have 3 qubits initially = |000>, what gates should I add and how to initialize those 3 qubits to set them to this form?

Yousef Zook
  • 105
  • 6

1 Answers1

1

Behind every array of $N$ qubits, there is an array of $2^N$ floats, each one of them is saving the amplitude $\alpha_{x_0...x_N}$ of the $|x_0...x_N \rangle$ state.

The coding behind initializing is just substituting $\alpha_{x_0...x_N}$ that you want, in the proper memory.

But this will be the illegal thing to do because it will not be physically possible.

The proper thing to do, is to initialize each qubit separately to $|0\rangle$ (in the simulation behind scene it will be init $\alpha_{0...0}=1$ and all other to $0$.

Now, to create more complicated states, you need to act with gates. for example, if you want to init $x_0$ to $|+\rangle$, you should apply $H$ on it.

EDIT:

To get more complicated states, you need to be creative. Achieve any state from $|000>$ state is not trivial at all, and this is why quantum algorithms are complicated and demand creative thinking.

The first stage is to try to decompose the 3 qubits, into 3 separate qubits. Which is not always possible (read about entanglement or states like $|00>+|11>$).

See this example of what I mean by decomposing:

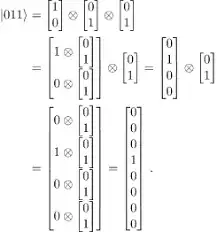
enter image description here

So, in your case it will is hard to find the coefficients that will construct such a state (maybe it can't decompose at all, and they are entangled):

$\frac{1}{\sqrt{8}}\begin{bmatrix} i/\sqrt{2} \\ 1 \\ (1+i)/\sqrt{2} \\ 0 \\ 0 \\ 1+2i \\ 1/\sqrt{2} \\ 0 \end{bmatrix}$

If it is decomposable, you can solve 8 equations (each row of the vector) with 6 variables (the $a_i|0>+b_i|1>$ of the 3 qubits).

In case it can't be decomposed, the only way to build them is using also gates that act on more than 1 qubit (like CNOT).

The matrix representation of all those gates is a (not unique) $8*8$ matrix, which represents a tensor product of operators on the 3 qubits space, which you also need to decompose.

BUT! The other way is easier, given $|000>$ state, you can act with any gate you like, and try to follow the state.

Also, cases like :

$\frac{1}{\sqrt{8}}\begin{bmatrix} 1\\1\\1\\1\\1\\1\\1\\1 \end{bmatrix}$

are easier to build. You can build it by applying $H$ gate on all the 3 qubits, which will make each one of them $\frac{1}{\sqrt{2}}\begin{bmatrix}1\\1 \end{bmatrix}$ so all the 3 together will give you equal superposition.

Another example is $H$ only on the first qubit, which will put you $\frac{1}{\sqrt{2}}(|000>+|100>)$

Once you will have a good understanding of what each gate is doing, you will be able to build different states. Most of the time, you will not need to build weird init states like the one you saw, it will be generally equal superpositioned states.

Ron Cohen
  • 1,522
  • 6
  • 24