I just want to know if there is a specific name for the implementation of a gate on the top qubit with the help of the bottom qubit, represented on this image:
It looks like gate teleportation but it is not as you do not need Bell states. The ancilla state is: $|A_{\theta}\rangle \equiv U_z(\theta) |+ \rangle$
You can find such circuit in this paper (page 28).
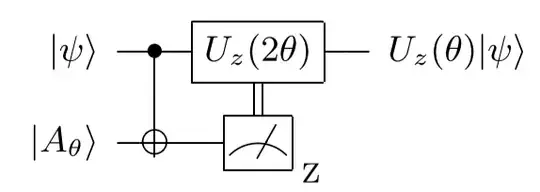
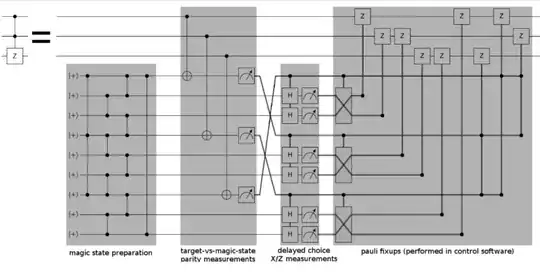
This is the circuit on which the magic state model is based. As they say in the linked paper, such a circuit is often called a gadget, more specifically a state injection gadget.
The reason why such gadgets are useful is that they allow to effectively implement a gate from the $k$-th level of the Clifford hierarchy using a special resource state and gates from the $(k-1)$-th level only. Originally, this was shown using actual gate teleportation circuits (see Gottesman and Chuang 1999). Later it was realised that for diagonal gates in the Clifford hierarchy, this primitive can be done without actually using teleportation, in particular without the use of Bell states (see Zhou, Leung, and Chuang 2000). Because of the historical origin, these gadget are sometimes called "(One-bit) gate teleportation", e.g. in Zeng, Chen, and Chuang 2008.
The resource state, $|A_\theta\rangle$ in your question, is called a magic state in this context. With help of magic states, universal fault-tolerant quantum computing is possible already for $k=3$. This is because the second level of the hierarchy is exactly the Clifford group which, together with any gate outside the group, yields an universal gate set. The famous choice $T=U_z(\pi/4)$ is in the third level of the Clifford hierarchy and can be implemented using a gadget and the magic state $|T\rangle = |0\rangle + e^{i\pi/4}|1\rangle$. The magic state model is fault-tolerant since Clifford gates can be made fault-tolerant using a suitable quantum code, and thus the state injection gadget is fault-tolerant, too.
I still call this gate teleportation. It's technically not quite right since the qubit doesn't move as part of applying the operation, it doesn't teleport, but it's basically the same. It's a few ZX calculus identities away. Basically it's like saying "instead of measuring A xor B and keeping B xor (B xor A), I measure A xor B and keep A".
You can see me using this style in eg. https://arxiv.org/abs/1905.08916
