How to construct a controlled $V$ gate in qiskit?

Question

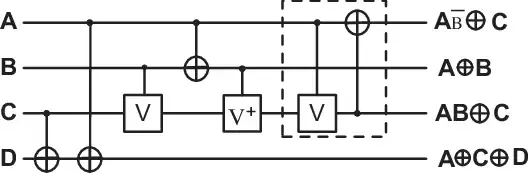
I have come across most of the quantum circuit which contains gate such as controlled $V$ and $V^{\dagger}$ but I dont know how to code it in Qiskit.

Answer 1

$V$ is the square root of $X$. That is,

\begin{align*} V = \sqrt X = \frac{1}{2}\left( {\begin{array}{*{20}{c}} {1 + i}&{1 - i}\\ {1 - i}&{1 + i} \end{array}} \right) \end{align*}

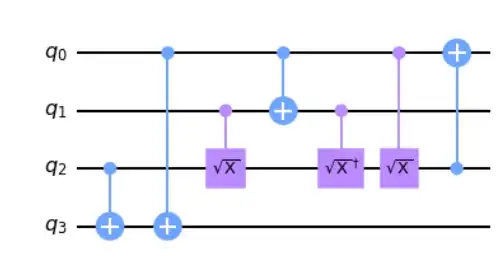
It is implemented in Qiskit with the name $SX$. So, the circuit in your question is easy to implement:

from qiskit import QuantumCircuit
from qiskit.circuit.library import SXdgGate
qc = QuantumCircuit(4)
qc.cx(2, 3)
qc.cx(0, 3)
qc.csx(1, 2)
qc.cx(0, 1)
csxdg_gate = SXdgGate().control()
qc.append(csxdg_gate, [1, 2])
qc.csx(0, 2)
qc.cx(2, 0)
qc.draw('mpl')

Answer 2

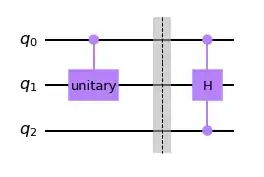
I don't remember what is the V-gate, sorry, but I created something that you can easily change so you can put any gate you like.

The idea is to create the gate and then use the ControlledGate to create the control you like. I also put on there an example of how to create a control from an already existing gate, notice you can put more than 1 control.

from qiskit.circuit import Gate
from qiskit.circuit.library import HGate
from qiskit.quantum_info import Operator
from qiskit import QuantumCircuit
my_control_gate = Operator([[1.,0],[0,-1]]).to_instruction().control(1)
circuit = QuantumCircuit(3)
circuit.append(my_control_gate, [0,1])
circuit.barrier()
H_control = HGate().control(2)
circuit.append(H_control, [0,2,1])
circuit.draw()

This code will give you this :

Hope it helps, tell me if you need precision :)